Linear Algebra
///
///
🏀

Camera Calibration: Direct Linear Transform

생성일
2022/01/28 04:49
태그
SVD
QR decomposition
DLT
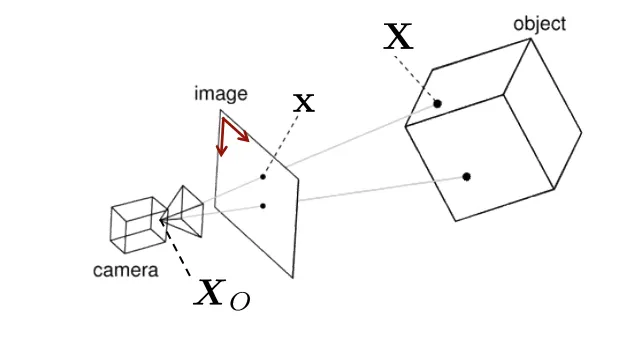
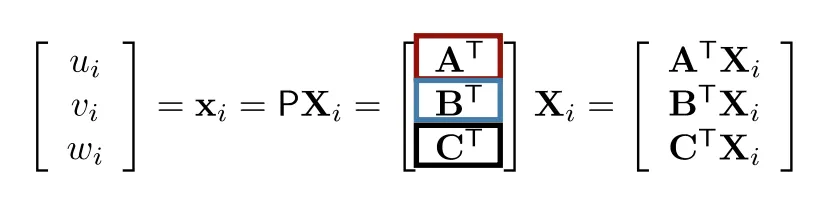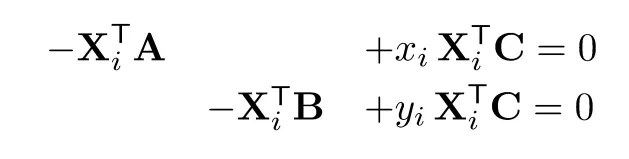저번 포스트에 다루었던 것은 world coordinate 에서 pixel coordinate 까지의 변환과정이었다.
x=PX\mathrm{x}=\mathrm{PX}
x → pixel coordinate / P → transformation / X → world coordinate
이제 변환 행렬 PP 의 파라미터들을 구하기 위해 어떠한 연산 과정을 거쳐야 할지 살펴보자.

Mapping 과정

•
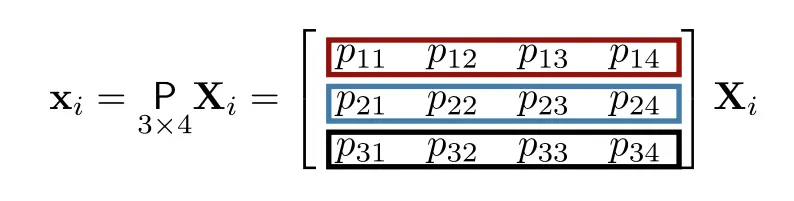
Direct Linear Transformation은 어떤 오브젝트의 점 X\mathbf{X} 가 이미지 점 x\mathbf{x} 로 매핑하는 것이다.
•
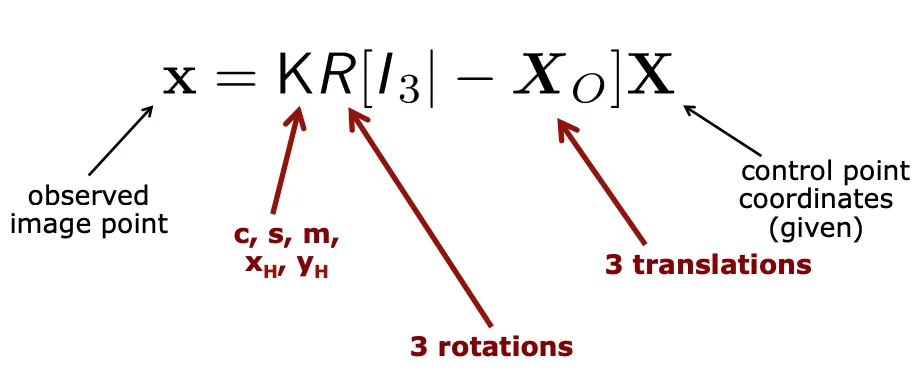
총 11개의 intrinsic 과 extrinsic parameter를 구해야한다.
•
Intrinsic의 경우 카매라 내부의 파라미터로써, 행렬 KK 로 주어진다.
•
Extrinsic의 경우 카메라의 위치와 방향을 나타내므로, 행렬 XOX_O 와 행렬 RR 의 조합으로 표현된다.

파라미터를 구하려면 몇 개의 Points가 필요할까?

11개의 미지수가 존재하고 affine camera를 모델링한다고 가정한다면, 적어도 6개의 점이 필요하다! (하나의 point가 두 개의 관찰값(x,y)을 주기 때문이다....) → DLT
그러나 만약 Calibrated Camera 인 경우 → Intrinsic parameter를 알고 있다! 6개의 미지수만 구하면 되고 적어도 3개의 점만 있으면 된다. → P3P

DLT 과정

목표 : 행렬 PP 의 11개의 파라미터 구하기
주어진 것 : (1) 점의 개수 I≥6I \geq 6 을 만족하는 오브젝트의 점 Xi\mathbf{X}_{i} (in 3D coordinates)의 집합 (2) xi=PXii=1,…,I\mathbf{x}_{i}={P} \mathbf{X}_{i} \quad i=1, \ldots, I 를 만족하는 이미지 좌표계에서의 점들의 집합 쉽게 말해 실제 위치상의 점과 이미지 상의 대응하는 점을 알고 있다는 이야기다.

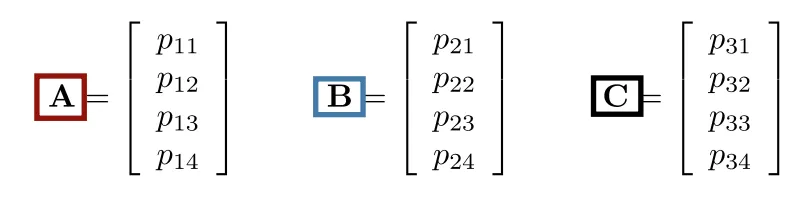
[1단계] 행렬 M 만들기

위와 같이 행렬 A,B,C를 만들게 되면 아래와 같이 주어진다.
xi=[xiyi1]=[uiviwi]=[A⊤XiB⊤XiC⊤Xi]\mathbf{x}_{i}=\left[\begin{array}{c}x_{i} \\y_{i} \\1\end{array}\right]=\left[\begin{array}{c}u_{i} \\v_{i} \\w_{i}\end{array}\right]=\left[\begin{array}{c}\mathbf{A}^{\top} \mathbf{X}_{i} \\\mathbf{B}^{\top} \mathbf{X}_{i} \\\mathbf{C}^{\top} \mathbf{X}_{i}\end{array}\right]
xi=uiwi=A⊤XiC⊤Xiyi=viwi=B⊤XiC⊤Xix_{i}=\frac{u_{i}}{w_{i}}=\frac{\mathbf{A}^{\top} \mathbf{X}_{i}}{\mathbf{C}^{\top} \mathbf{X}_{i}} \quad y_{i}=\frac{v_{i}}{w_{i}}=\frac{\mathbf{B}^{\top} \mathbf{X}_{i}}{\mathbf{C}^{\top} \mathbf{X}_{i}}
위에 제시된 식을 다시 표현하면 방정식의 형태로 표현하면
우리가 구하고자 하는 행렬 P의 원소들을 (12∗1)12 *1) 형태로 만든 column-vector를 만든다 (구하고자 하는 해)
p=(pk)=[ABC]=vec⁡(P⊤)\boldsymbol{p}=\left(p_{k}\right)=\left[\begin{array}{l}\mathbf{A} \\\mathbf{B} \\\mathbf{C}\end{array}\right]=\operatorname{vec}\left(\mathrm{P}^{\top}\right)
앞서 제시했던 식을 해를 구하는 형태로 만들기 위해 변형하면,
axi⊤p=0ayi⊤p=0\begin{aligned}\boldsymbol{a}_{x_{i}}^{\top} \boldsymbol{p} &=0 \\\boldsymbol{a}_{y_{i}}^{\top} \boldsymbol{p} &=0\end{aligned}
axi⊤=(−Xi⊤,0⊤,xiXi⊤)=(−Xi,−Yi,−Zi,−1,0,0,0,0,xiXi,xiYi,xiZi,xi)ayi⊤=(0⊤,−Xi⊤,yiXi⊤)=(0,0,0,0,−Xi,−Yi,−Zi,−1,yiXi,yiYi,yiZi,yi)\begin{aligned}\boldsymbol{a}_{x_{i}}^{\top} &=\left(-\mathbf{X}_{i}^{\top}, \mathbf{0}^{\top}, x_{i} \mathbf{X}_{i}^{\top}\right) \\&=\left(-X_{i},-Y_{i},-Z_{i},-1,0,0,0,0, x_{i} X_{i}, x_{i} Y_{i}, x_{i} Z_{i}, x_{i}\right) \\\boldsymbol{a}_{y_{i}}^{\top} &=\left(\mathbf{0}^{\top},-\mathbf{X}_{i}^{\top}, y_{i} \mathbf{X}_{i}^{\top}\right) \\&=\left(0,0,0,0,-X_{i},-Y_{i},-Z_{i},-1, y_{i} X_{i}, y_{i} Y_{i}, y_{i} Z_{i}, y_{i}\right)\end{aligned}
아래와 같이 우리가 흔히 보던 Linear system으로 치환 가능하고 이제 이문제는 아래 식을 만족하는 해를 구하는 문제로 바뀌게 된다.
[ax1⊤ay1⊤⋯axi⊤ayi⊤⋯axI⊤ayI⊤]p=M2I×12p12×1=!0\left[\begin{array}{c}\boldsymbol{a}_{x_{1}}^{\top} \\\boldsymbol{a}_{y_{1}}^{\top} \\\cdots \\\boldsymbol{a}_{x_{i}}^{\top} \\\boldsymbol{a}_{y_{i}}^{\top} \\\cdots \\\boldsymbol{a}_{x_{I}}^{\top} \\\boldsymbol{a}_{y_{I}}^{\top}\end{array}\right] \boldsymbol{p}=\underset{2 I \times 12}{\mathrm{M}} \underset{12 \times 1}{\boldsymbol{p}} \stackrel{!}{=} 0

[2단계] SVD를 이용하여 행렬 P 구하기

•
Ax=0Ax = \mathbf{0} 의 꼴의 linear equation의 해를 구하는 것은 행렬 AA의 null space를 찾는 것과 같다.
•
Mp=!0M p \stackrel{!}{=} 0 를 풀기 위해 SVD를 사용한다
•
singular value 값 0에 해당하는 가장 작은 singular vector가 pp가 된다

정확하지 않은 관측값이 존재하는 경우가 있기 때문에, 오차를 가장 작게 하는 행렬 pp 를 찾아야 한다.

Mp=w\mathrm{M} \boldsymbol{p}=\boldsymbol{w}
Ω=w⊤wp^=arg⁡min⁡pw⊤w=arg⁡min⁡pp⊤M⊤Mp∥P∥2=∑ijpij2=∥p∥=1\begin{aligned}\Omega &=\boldsymbol{w}^{\top} \boldsymbol{w} \\\widehat{\boldsymbol{p}} &=\arg \min _{\boldsymbol{p}} \boldsymbol{w}^{\top} \boldsymbol{w} \\&=\arg \min _{\boldsymbol{p}} \boldsymbol{p}^{\top} \mathrm{M}^{\top} \mathrm{M} \boldsymbol{p}\end{aligned} \\\|P\|_{2}=\sum_{i j} p_{i j}^{2}=\|\boldsymbol{p}\|=1
SVD를 이용하면 아래와 같이 분해할 수 있으며,
M2I×12=U2I×12 S12×12V⊤12×12=∑i=112siuivi⊤\underset{2 I \times 12}{\mathrm{M}}=\underset{2 I \times 12}{U} \underset{12 \times 12}{\mathrm{~S}} \underset{12 \times 12}{V^{\top}}=\sum_{i=1}^{12} s_{i} \boldsymbol{u}_{i} \boldsymbol{v}_{i}^{\top}
이 때 가장 작은 singular value에 해당하는 singular vector를 pp로 풀면 된다.

[3단계] 행렬 P를 분해하여 각 파라미터들 구하기

•
어떻게 행렬 PP 를 가지고 K,R,XO\mathrm{K}, R, \boldsymbol{X}_{O} 를 구할 것 인가?
행렬 PP 는 아래와 같은 형태로 나눠서 표현할 수 있다.
P=[KR∣−KRXO]=[H∣h]H=KRh=−KRXO\mathrm{P}=\left[\mathrm{K} R \mid-\mathrm{K} R \boldsymbol{X}_{O}\right]=[\mathrm{H} \mid \mathbf{h}] \\\mathrm{H}=\mathrm{K} R \quad \mathbf{h}=-\mathrm{K} R \mathbf{X}_{O}
공통된 부분을 통해 우린 간단히 Projection Center XO\boldsymbol{X}_{O} 를 구할 수 있다.
XO=−H−1h\boldsymbol{X}_{O}=-\mathrm{H}^{-1} \mathbf{h}
그렇다면 K,R\mathrm{K}, R 은 어떻게 구할 것인가?? 일단 구하기전 각 행렬들의 특징을 살펴보는 것이 중요한데
•
행렬 K\mathrm{K} 는 triangular matrix 의 형태를 가진다.
•
행렬 RR은 roatation matrix 이다. RT=R−1R^{\mathrm{T}}=R^{-1} 의 성질을 가진다.
위의 성질들을 잘 살펴보면 QR decomposition을 통해 각 파라미터를 구할 수 있을 거라는 생각이 든다.
H−1=(KR)−1=R−1 K−1=R⊤K−1\mathrm{H}^{-1}=(\mathrm{K} R)^{-1}=R^{-1} \mathrm{~K}^{-1}=R^{\top} \mathrm{K}^{-1}
왼쪽이 Q, 오른쪽이 R의 형태를 띈다.
위와 같이 구하게 되면 양수의 diagonal elements를 얻게 되는데, 만약 음수 값을 얻고 싶다면 아래와 같이 구하면 된다.
K←KR(z,π)R←R(z,π)RR(z,π)=[−1000−10001]\mathrm{K} \leftarrow \mathrm{K} R(z, \pi) \quad R \leftarrow R(z, \pi) R \\ R(z, \pi)=\left[\begin{array}{ccc} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{array}\right]
앞서 제시한 행렬 H=KR \mathrm{H}=\mathrm{K} R 은 homogenous 한 상태이기 때문에, 다시 normalize 해주는 과정이 필요하다.
K←1K33KK \leftarrow \frac{1}{K_{33}} K
Made with