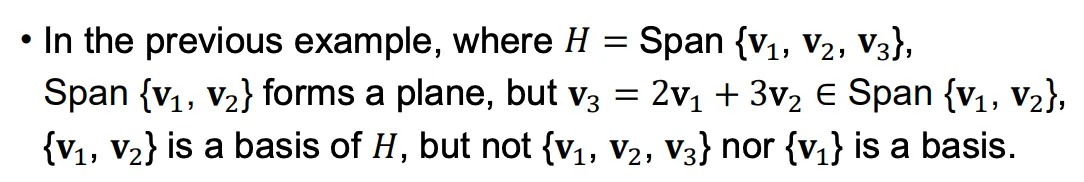슬램과 함께 춤을

Linear Algebra

1. Linear Equation and Linear System

슬램과 함께 춤을

Linear Algebra

1. Linear Equation and Linear System

🛣️

1. Linear Equation and Linear System

태그

span

Independence

Transformation

Linear Equation

linear equation은 변수

x_1,\cdot\cdot\cdot, x_n

이 아래와 같은 형태로 작성될 수 있는 방정식이다.

a_{1} x_{1}+a_{2} x_{2}+\cdots+a_{n} x_{n}=b

b

와 계수

a_1,\cdot\cdot\cdot, a_n

은 실수 혹은 복소수이고 위의 방정식은 다음과 같이 작성된다,

\mathbf{a}^{T} \mathbf{x}=b \\ \text { where } \mathbf{a}=\left[\begin{array}{c}a_{1} \\a_{2} \\\vdots \\a_{n}\end{array}\right] \text { and } \mathbf{x}=\left[\begin{array}{c}x_{1} \\x_{2} \\\vdots \\x_{n}\end{array}\right] \text {. }

Linear System

변수

x_1,\cdot\cdot\cdot, x_n

을 포함하여 하나 이상의 linear equations를 모은 집합이다

\mathbf{A} \mathbf{x}=\mathbf{b}

Identity Matrix

Identity matrix는 square matrix이고 diagonal entries가 모두 1인 행렬이다. 그리고 그 부분을 제외한 나머지가 0이다.

I_{n} \in \mathbb{R}^{n \times n}\\ I_{3}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]

이러한 Identity matrix는 어떤 임의의 벡터

x \in \mathbb{R}^n

에 행렬

I_n

을 곱하면 자기 자신이 도출된다.

\forall \mathbf{x} \in \mathbb{R}^{n}, \quad I_{n} \mathbf{x}=\mathbf{x}

Inverse Matrix

임의의 square matrix

A \in \mathbb{R}^{n \times n}

의 inverse matrix

A^{-1}

는 아래 식을 만족한다.

A^{-1} A=A A^{-1}=I_{n}

2 \times 2

matrix

A=\left[\begin{array}{ll}a & b \\c & d\end{array}\right]

에 대한 역행렬

A^{-1}

은 아래와 같이 정의된다.

A^{-1}=\frac{1}{a d-b c}\left[\begin{array}{cc}d & -b \\-c & a\end{array}\right]

Linear System을 Inverse Matrix를 이용해 풀이하기

앞서 제시한 Linear System

\mathbf{A} \mathbf{x}=\mathbf{b}

는 다음과 같은 과정을 통해 풀이가 가능하다

\begin{array}{c}A \mathbf{x}=\mathbf{b} \\A^{-1} A \mathbf{x}=A^{-1} \mathbf{b} \\I_{n} \mathbf{x}=A^{-1} \mathbf{b} \\\mathbf{x}=A^{-1} \mathbf{b}\\ \text{(unique solution)}\end{array}

만약 matrix

A

가 invertible 하지 않다면,

\operatorname{det} A

의 값이 0이되고, 해가 무수히 많거나 해가 없는 경우가 된다.

Linear Combination

vectors

\mathbf{v}_{1}, \mathbf{v}_{2}, \cdots, \mathbf{v}_{p} \text { in } \mathbb{R}^{n}

이 주어지고 scalars

c_{1}, c_{2}, \cdots, c_{p}

가 주어질 때,

c_{1} \mathbf{v}_{1}+\cdots+c_{p} \mathbf{v}_{p}

가중치 계수를

c_{1}, c_{2}, \cdots, c_{p}

로 하면서

\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}

의 Linear Combination이라고 한다. weights는 0을 포함한 어떠한 실수값도 가질수 있다.

Vector Equation Form

\begin{array}{c}{\left[\begin{array}{lll}60 & 5.5 & 1 \\65 & 5.0 & 0 \\55 & 6.0 & 1\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]=\left[\begin{array}{l}66 \\74 \\78\end{array}\right]} \\\mathbf{Ax}=\mathbf{b}\end{array}

\begin{array}{c}{\left[\begin{array}{l}60 \\65 \\55\end{array}\right] x_{1}+\left[\begin{array}{l}5.5 \\5.0 \\6.0\end{array}\right] x_{2}+\left[\begin{array}{l}1 \\0 \\1\end{array}\right] x_{3}=\left[\begin{array}{l}66 \\74 \\78\end{array}\right]} \\\mathbf{a}_{1} x_{1}+\mathbf{a}_{2} x_{2}+\mathbf{a}_{3} x_{3}=\mathbf{b}\end{array}

첫번째 형태가 Matrix Equation이고, 두번째 형태가 Vector Equation의 형태이다. 이러한 형태로 변형하는 이유는 Linear Equation이 해를 가지는 지를 판별하기에 용이하기 때문이다. 이 때 판별하는데 사용되는 개념이 밑에 제시할 Span이다.

Span

vectors

\mathbf{v}_{1}, \mathbf{v}_{2}, \cdots, \mathbf{v}_{p} \text { in } \mathbb{R}^{n}

이 주어지고,

\operatorname{Span}\left\{\mathrm{v}_{1}, \cdots, \mathrm{v}_{p}\right\}

은 모든

\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}

의 Linear Combination의 집합으로 정의한다.

c_{1} \mathbf{v}_{1}+c_{2} \mathbf{v}_{2} \cdots+c_{p} \mathbf{v}_{p}

이 때 scalars

c_{1}, c_{2}, \cdots, c_{p}

는 임의의 값이다.

subset of

\mathbb{R}^{n}

spanned by

\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}

라고 부르기도 한다.

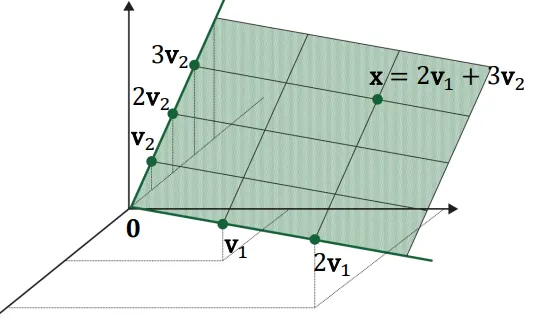
기하학적으로 Span을 묘사하면 다음과 같다.

\operatorname{Span}\left\{\mathrm{v}_{1}, \mathrm{v}_{2}\right\}

은

\mathbb{R}^3

상의 평면으로 묘사할 수 있다. (

\mathbf{v}_{1}, \mathbf{v}_{2}, 0

모두 포함한다)

\\\mathbf{a}_{1} x_{1}+\mathbf{a}_{2} x_{2}+\mathbf{a}_{3} x_{3}=\mathbf{b}

의 식에서. 해가 존재하기 위해서는

\mathbf{b} \in \operatorname{Span}\left\{\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}\right\}

을 만족해야한다. (얻고자 하는 해가 저 평면위에 존재해아 한다는 뜻!)

해가 존재하는지는 확인할 수 있었다. 그런데 해가 유일한지 무수히 많은지는 다시 확인해봐야한다. 아래 개념들을 통해서.

Linear Independence

실용적인 정의

vectors

\mathbf{v}_{1}, \cdots, \mathbf{v}_{p} \in \mathbb{R}^{n}

이 주어졌을 때,

\mathbf{v}_{j}

가 그 전의 vectors

\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{j-1}\right\}

의 Linear Combination의 형태로 표현되는지 확인한다.

\mathbf{v}_{j} \in \operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{j-1}\right\} \text { for some } j=1, \ldots, p ?

만약

\mathbf{v}_{j}

가 Linear Combination으로 표현이 된다면 linearly dependent이고, 그렇지 않다면 linearly Independent한 것이다.

Linear Dependence

행렬

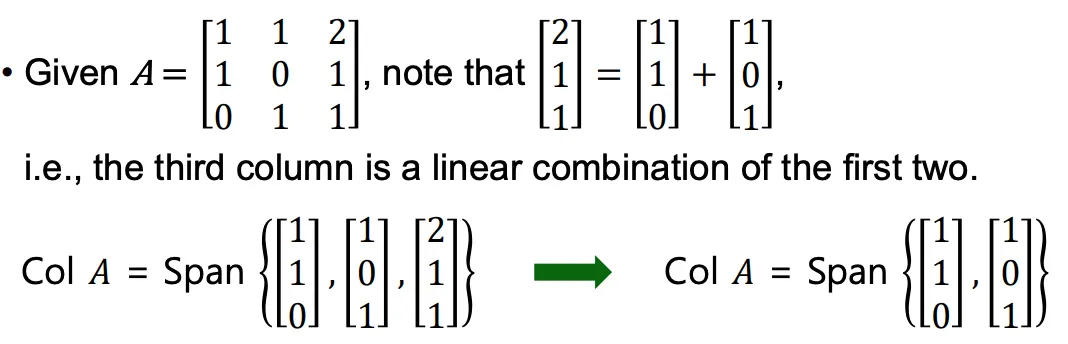
\mathbf{A}

의 column vectors들

\mathbf{a}_{1}, \mathbf{a}_{2}, \cdots, \mathbf{a}_{n}

이 linearly dependent한 경우 Span을 늘리지 않게된다.

\text { If } \mathbf{v}_{3} \in \operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\} \text {, then } \\ \text {Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\}=\operatorname{Span}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}\right\}

vector

\mathbf{v}_{3}

는

\mathbf{v}_{1}, \mathbf{v}_{2}

를 linear combination하여 표현할 수 있기 때문에

\mathbf{v}_{1}, \mathbf{v}_{2}, \mathbf{v}_{3}

의 조합은 사실상

\mathbf{v}_{1}, \mathbf{v}_{2}

의 조합과 같기 때문에 span을 늘리지 않는다.

Uniqueness of Solution for $A\mathbf{x} = \mathbf{b}$

\begin{array}{c}{\left[\begin{array}{l}60 \\65 \\55\end{array}\right] x_{1}+\left[\begin{array}{l}5.5 \\5.0 \\6.0\end{array}\right] x_{2}+\left[\begin{array}{l}1 \\0 \\1\end{array}\right] x_{3}=\left[\begin{array}{l}66 \\74 \\78\end{array}\right]} \\\mathbf{a}_{1} x_{1}+\mathbf{a}_{2} x_{2}+\mathbf{a}_{3} x_{3}=\mathbf{b}\end{array}

앞서 제시한 식을 다시보면

\mathbf{a}_{1}, \mathbf{a}_{2}, \mathbf{a}_{3}

가 모두 linearly independent 할 때 유일한 해를 가지며 만약 linearly dependent하다면 해는 무수히 많게 된다.

Subspace

subspace

H

는

\mathbb{R}^{n}

의 linear combination에 대해 닫혀 있는 부분집합으로 정의된다.

•

어떠한 두 벡터 u1,u2∈H\mathbf{u_1},\mathbf{u_2} \in Hu1​,u2​∈H와 임의의 스칼라 값 c,dc, dc,d 가 주어질 때,
cu1+du2∈Hc \mathbf{u}_{1}+d \mathbf{u}_{2} \in Hcu1​+du2​∈H 를 만족한다.

•

subspace는 항상 Span⁡{v1,⋯ ,vp}\operatorname{Span}\left\{\mathbf{v}_{1}, \cdots, \mathbf{v}_{p}\right\}Span{v1​,⋯,vp​} 의 꼴로 나타내어 진다.

Basis (of subspace)

subspace

H

의 basis는 아래 조건을 만족하는 벡터의 집합이다.

•

주어진 subspace HHH 를 완전히 span해야 한다.

•

중복 없이 Linearly independent하다.

•

basis는 한 개가 아니며 수 많은 basis를 만들 수 있다. → not unique

Dimension (of subspace)

그렇다면 subspace

H

가 주어지면 어떤 것이 unique 하다고 말할 수 있을까? 바로

H

를 구성하는 basis의 개수는 항상 유일하다! 이 것이 바로 dimension의 정의이다.

\text { the number of vectors in any basis for } H = \operatorname{dim} H

Column Space of Matrix

행렬

A

의 column space는

A

의 column들로 spanned된 subspace를 의미한다. 이러한 것을

\operatorname{Col}A

라고 부른다.

Rank

행렬

A

의 rank는 행렬

A

의 column space의 dimension을 의미한다.

\operatorname{rank} A=\operatorname{dim} \operatorname{Col} A

Transformation

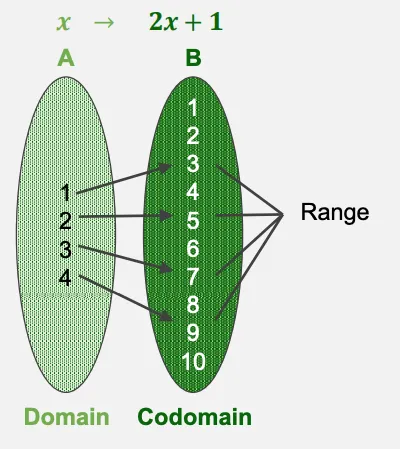
transformation(혹은 function, mapping)

T

는 입력

x

를 출력

y

로 매핑하는 것을 의미한다.

T: x \mapsto y

•

domain : 입력 xxx 의 가능한 모든 값의 집합

•

co-domain : 출력 yyy 의 가능한 모든 값의 집합

•

image : 입력 xxx 가 주어졌을 때, 매핑되어 나오는 출력 yyy 

•

range : domain 내에 존재하는 각 입력들의 출력 값의 집합

•

임의의 입력 xxx 에 대응하는 출력은 오직 하나이다.

Linear Transformation

transformation

T

이 linear하기 위해서는 아래 조건을 만족해야한다.

T(c \mathbf{u}+d \mathbf{v})=c T(\mathbf{u})+d T(\mathbf{v}) \\\text { for all } \mathbf{u}, \mathbf{v} \text { in the domain of } T \text { and for all scalars } c \text { and } d

일반적으로,

T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}

를 linear transformation 이라고 가정한다면,

T

는 항상 matrix-vector multiplication 형태로 나타내어 진다.

T(\mathbf{x})=A \mathbf{x} \text { for all } \mathbf{x} \in \mathbb{R}^{n}

행렬

A \in \mathbb{R}^{m \times n}

의

j

번째 column은 벡터

T\left(\mathbf{e}_{j}\right)

와 같으며,

\mathbf{e}_{j}

는

\mathbb{R}^{n \times n}

ldentity Matrix의

j

번째 column이라고 한다.

A=\left[\begin{array}{lll}T\left(\mathbf{e}_{1}\right) & \cdots & T\left(\mathbf{e}_{n}\right)\end{array}\right]

행렬

A

를 linear transformation

T

의 standard matrix 라고 부른다.

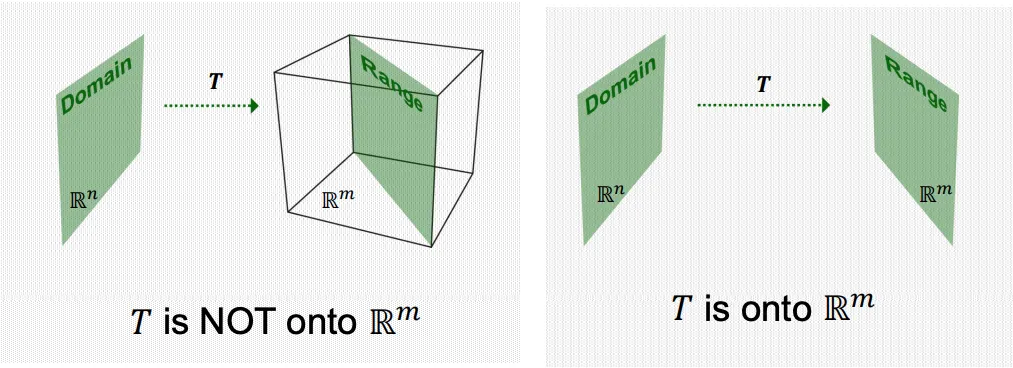
Onto

매핑

T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}

을 가정했을 때,

x \in \mathbb{R}^{n}

중 적어도 하나에 대한 image가

\mathbf{b} \in \mathbb{R}^{m}

에 존재할 때 즉, range 가 co-domain 과 동일할 때 (치역 = 공역) onto라고 정의한다.

일반적으로 입력 차원

n

이 출력 차원

m

보다 크다면, onto 를 만족할 가능성이 높다, 하지만 반대의 경우 절대 onto를 만족할 수가 없다.

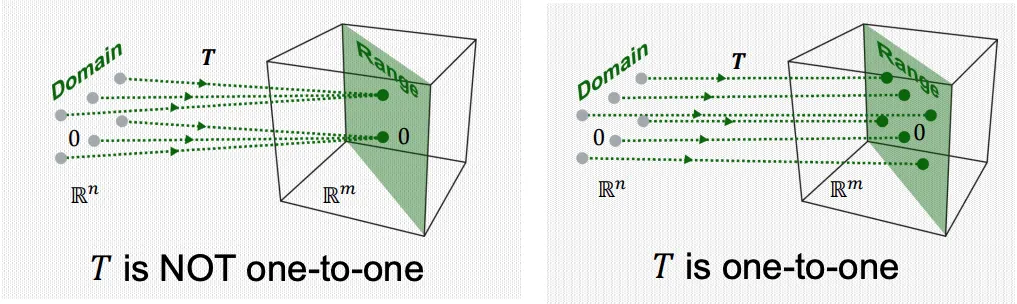
One to One

매핑

T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}

을 가정했을 때, image

\mathbf{b} \in \mathbb{R}^{m}

에 대응하는

x \in \mathbb{R}^{n}

이 반드시 하나일 때 one-to-one 이라고 가정한다. 즉, range 안의 각각의 출력 벡터가 반드시 오직 하나의 입력 벡터로부터 매핑 되어야 한다는 것이다.

정리하면,

매핑

T: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}

을 linear transformation으로 가정하면, 아래 식을 만족하게 되고

T(\mathrm{x})=A \mathrm{x} \text { for all } \mathrm{x} \in \mathbb{R}^{n}

행렬

A

의 column vector들이 linearly independent 하다면 one-to-one 하다.

행렬

A

의 column vector들의 span이

\mathbb{R}^{m}

이라면 onto이다.

reference

Linear Transformation & onto, ono-to-one의 개념

아래 내용은 김도형 박사님의 선형대수 강의안, edwith의 인공지능을 위한 선형대수 강의와 KOCW의 한양대학교 이상화 교수님의 선형대수학 강의를 보고 정리한 내용이다. 행렬에 의해서의 변환 또는 함수에 대해 정리해 볼 것이다. Transformation Domain(정의역) : 입력값으로 가질 수 있는 모든 값들의 집합 Co-domain(공역)

인공지능을 위한 선형대수 오리엔테이션 : edwith

인공지능을 위한 선형대수

1. Linear Equation and Linear System

Linear Equation

Linear System

Identity Matrix

Inverse Matrix

Linear System을 Inverse Matrix를 이용해 풀이하기

Linear Combination

Vector Equation Form

Span

해가 존재하는지는 확인할 수 있었다. 그런데 해가 유일한지 무수히 많은지는 다시 확인해봐야한다. 아래 개념들을 통해서.

Linear Independence

Linear Dependence

Uniqueness of Solution for Ax=bA\mathbf{x} = \mathbf{b}Ax=b

Subspace

Basis (of subspace)

Dimension (of subspace)

Column Space of Matrix

Rank

Transformation

Linear Transformation

Onto

One to One

reference

Uniqueness of Solution for $A\mathbf{x} = \mathbf{b}$