Linear Algebra
///
///
🎩

Relative Orientation, Fundamental and Essential Matrix

생성일
2022/02/14 05:16
태그
Coplanarity
지금까지 카메라 하나를 가지고 여러 활동들을 해보았다. 이제는 카메라 2개를 가지고 3D world를 표현해보자! 이제부터 우리는 2개의 이미지를 가지고 있다는 상황을 고려할 것이다.

Camera Pair

카메라 쌍을 이용하는 방법은 크게 두가지가 존재한다.
1.
A stereo camera → 2 대의 카메라를 좌우로 붙여 놓은 것으로 보통 두개의 렌즈를 가지고 있다.
2.
One camera that moves → 한 대의 카메라를 옮겨가며 하나의 오브젝트를 촬영하기

Camera pair = two configurations from which images have been taken

Orientation Parameters

카메라 쌍의 orientation은 개별 카메라의 orientation을 이용해 표현할 수 있다. Orientation을 설명하는 파라미터들의 종류와 개수를 알아보자!
•
Calibrated cameras : (3 for rotation, 3 for translation * 2 for camera pairs) 총 12개의 파라미터가 필요하다. 앞서 다룬 spatial resection / P3P 과정을 통해 각각의 카메라의 Extrinsic parameter를 구하면 된다. 3~4개의 control points가 필요하다.
•
Uncalibrated cameras : ([5 intrinsic + 3 for rotation + 3 for translation] * 2 for camera pairs) 총 22개의 파라미터가 필요하다. 앞서 다룬 DLT 과정을 통해 각각의 카메라의 Extrinsic + Intrinsic parameter를 구하면 된다. 6개의 control points가 필요하다.

어떠한 파라미터를 얻을 수 있을까?

얻을 수 없는 것

•
Global한 translation과 rotation은 알 수가 없다.
•
scale 정보는 알 수가 없다.

얻을 수 있는 것

•
1번째 카메라에 관한 2번째 카메라의 상대적인 rotation matrix RR (3 params)
•
center of projection을 잇는 선의 방향 BB (2 params) → BB 의 길이는 알수가 없다.

Calibrated Camera라고 가정한다면,

12개의 파라미터 중 1번째 카메라의 rotation(3), translation(3), 카메라 사이의 길이(1). 총 7개의 파라미터를 제외한 5개의 파라미터를 얻을 수 있다!

Photogrammetric Model

•
2개의 카메라 이미지가 주어졌을 때, 오브젝트를 reconstruct 하는 것을 similarity transform까지만 구할 수 있다.
•
orientation of photogrammetric model은 absolute orientation이라고 한다.
•
absolute orientation를 얻기 위해선 적어도 3 points in 3D가 필요하다 (→ 7개의 파라미터 추정위해)

Uncalibrated Camera라고 가정한다면,

•
Straight-line Preserving 하지만 angle-preserving하지는 않습니다
•
Projective Transform을 합니다 (15개의 파라미터를 얻는다)
•
22 - 15 = 7 개의 파라미터를 두개의 이미지 쌍으로 부터 얻습니다.
•
Absolute Orientation을 위해 최소 5개 이상의 3D 점이 필요합니다.
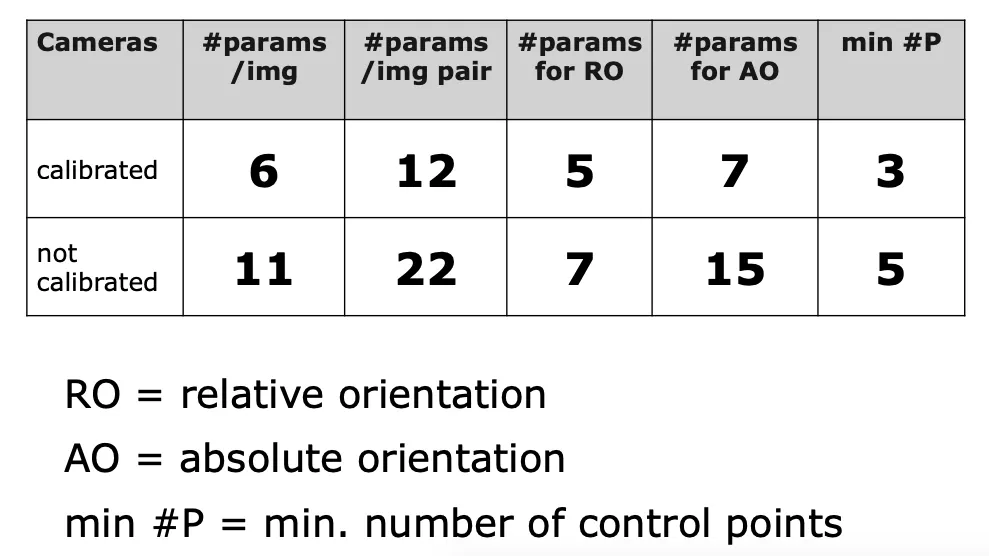
위의 내용을 표로 정리하면 아래와 같습니다.

Coplanarity Constraint for Uncalibrated Cameras

•
Straight-Line Preserving한 카메라를 가정한다. → uncalibrated camera이다.
coplanarity constraint를 구하기 위해서 가정하는 상황이 아래와 같다.
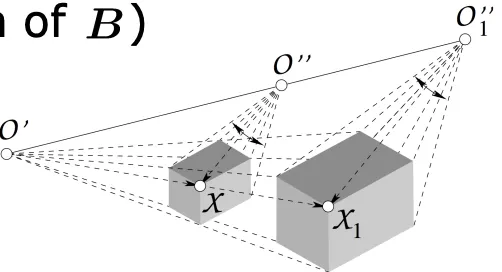
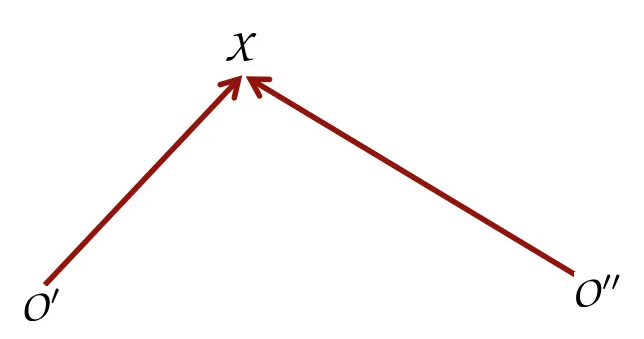
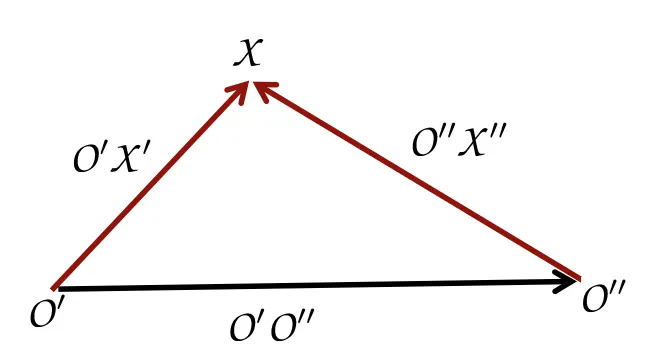
2개의 카메라로 바라보는 object를 점 XX로 표현하고, O′,O′′O^{\prime}, O^{\prime\prime} 은 각각의 카메라의 projection center를 의미합니다. 2개의 카메라에서 나오는 ray의 교차점이 점 XX가 되는 완벽한 orientation을 가정합니다. O′,O′′O^{\prime}, O^{\prime\prime}를 잇는 선을 이으면 ray들이 3D 안의 평면에 놓여져 있다는 것을 알수 있습니다. 이것이 바로 coplanarity constraint의 시작입니다!

Scalar Triple Product

이 때 이 coplanarity constraint를 수학적으로 표현하기 위해 사용하는 연산입니다.
[A,B,C]=(A×B)⋅C[A, B, C]=(A \times B) \cdot C
3개의 vector가 parallelepiped 된 것의 부피를 나타냅니다. 라고 적혀있지만 가장 중요한 이 연산은 목적은 주어진 3벡터가 같은 평면상에 있는가? 를 판별하는 것입니다.
[A,B,C]=0[A, B, C]=0 을 만족한다면 3개의 벡터가 모두 한 평면 위에 있다고 생각할 수 있습니다.
따라서 우리는 아까 가정에 의해 projection Centers와 오브젝트의 점이 이루는 평면을 이뤄야 하므로 아래 식이 필연적으로 성립하게 됩니다.
[O′X′O′O′′O′′X′′]=0\left[\begin{array}{lll}O^{\prime} X^{\prime} & O^{\prime} O^{\prime \prime} & O^{\prime \prime} X^{\prime \prime}\end{array}\right]=0
이 방정식을 풀기 위해 우리는 O′X′,O′′X′′O^{\prime} X^{\prime}, O^{\prime\prime} X^{\prime\prime}을 이미지 좌표계 x′,x′′\mathbf{x}^{\prime}, \mathbf{x}^{\prime\prime}을 이용해 표현해야 합니다. 이를 위해 Projection Matrix PP 를 이용하겠습니다.
x′=P′Xx′′=P′′XP′=K′R′[I3∣−XO′]P′′=K′′R′′[I3∣−XO′′]\mathbf{x}^{\prime}=P^{\prime} \mathbf{X} \quad \mathbf{x}^{\prime \prime}=P^{\prime \prime} \mathbf{X} \\\mathrm{P}^{\prime}=\mathrm{K}^{\prime} R^{\prime}\left[\boldsymbol{I}_{3} \mid-\boldsymbol{X}_{O^{\prime}}\right] \quad \mathrm{P}^{\prime \prime}=\mathrm{K}^{\prime \prime} R^{\prime \prime}\left[\boldsymbol{I}_{3} \mid-\boldsymbol{X}_{O^{\prime \prime}}\right]
이를 이미지 평면상의 점으로 부터 구하기 위해 아래의 식을 이용합니다. (normalized direction입니다.)
nx′=(R′)−1( K′)−1x′nx′′=(R′′)−1( K′′)−1x′′{ }^{n} \mathbf{x}^{\prime}=\left(R^{\prime}\right)^{-1}\left(\mathrm{~K}^{\prime}\right)^{-1} \mathbf{x}^{\prime} \\ { }^{n} \mathbf{x}^{\prime \prime}=\left(R^{\prime \prime}\right)^{-1}\left(\mathrm{~K}^{\prime \prime}\right)^{-1} \mathbf{x}^{\prime \prime}
위 식은 아래와 같습니다.
nx′=[I3∣−XO′]Xnx′′=[I3∣−XO′′]X{ }^{n} \mathbf{x}^{\prime}=\left[\boldsymbol{I}_{3} \mid-\boldsymbol{X}_{O^{\prime}}\right] \mathbf{X} \\ { }^{n} \mathbf{x}^{\prime\prime}=\left[\boldsymbol{I}_{3} \mid-\boldsymbol{X}_{O^{\prime\prime}}\right] \mathbf{X}
base vector O′,O′′O^{\prime}, O^{\prime\prime} 는 projection center의 좌표계를 통해 얻을 수 있습니다.
b=XO′′−XO′\boldsymbol{b}=\boldsymbol{X}_{O^{\prime \prime}}-\boldsymbol{X}_{O^{\prime}}
아까 구한, [O′X′O′O′′O′′X′′]=0\left[\begin{array}{lll}O^{\prime} X^{\prime} & O^{\prime} O^{\prime \prime} & O^{\prime \prime} X^{\prime \prime}\end{array}\right]=0의 요소들을 대체하여 구해보면,
[nx′bnx′′]=0nx′⋅(b×nx′′)=0nx′⊤Sbnx′′=0\begin{aligned}\left[{ }^{n} \mathbf{x}^{\prime} \quad \boldsymbol{b} \quad{ }^{n} \mathbf{x}^{\prime \prime}\right] &=0 \\{ }^{n} \mathbf{x}^{\prime} \cdot\left(\boldsymbol{b} \times{ }^{n} \mathbf{x}^{\prime \prime}\right) &=0 \\{ }^{n} \mathbf{x}^{\prime \top} S_{b}{ }^{n} \mathbf{x}^{\prime \prime} &=0\end{aligned}
여기서 SbS_{b} 는 skew-symmetric matrix로써 벡터의 외적을 행렬의 곱의 형태로 표현한다.
앞에서 구한 normalized direction를 이용하여 위의 식과 결합하면 아래와 같이 표현할 수 있다.
x′⊤(K′)−⊤(R′)−⊤Sb(R′′)−1( K′′)−1x′′=0\mathbf{x}^{\prime \top}\left(\mathrm{K}^{\prime}\right)^{-\top}\left(R^{\prime}\right)^{-\top} S_{b}\left(R^{\prime \prime}\right)^{-1}\left(\mathrm{~K}^{\prime \prime}\right)^{-1} \mathbf{x}^{\prime \prime}=0
x′⊤(K′)−⊤(R′)−⊤Sb(R′′)−1( K′′)−1⏟Fx′′=0\mathbf{x}^{\prime \top} \underbrace{\left(\mathrm{K}^{\prime}\right)^{-\top}\left(R^{\prime}\right)^{-\top} S_{b}\left(R^{\prime \prime}\right)^{-1}\left(\mathrm{~K}^{\prime \prime}\right)^{-1}}_{\mathrm{F}} \mathrm{x}^{\prime \prime}=0
F=(K′)−⊤(R′)−⊤Sb(R′′)−1( K′′)−1=(K′)−⊤R′SbR′′⊤(K′′)−1\begin{aligned}\mathrm{F} &=\left(\mathrm{K}^{\prime}\right)^{-\top}\left(R^{\prime}\right)^{-\top} \mathrm{S}_{b}\left(R^{\prime \prime}\right)^{-1}\left(\mathrm{~K}^{\prime \prime}\right)^{-1} \\&=\left(\mathrm{K}^{\prime}\right)^{-\top} R^{\prime} \mathrm{S}_{b} R^{\prime \prime \top}\left(\mathrm{K}^{\prime \prime}\right)^{-1}\end{aligned}
x′⊤Fx′′=0\mathbf{x}^{\prime \top} \mathrm{F} \mathbf{x}^{\prime \prime}=0

위와 같은 식을 coplanarity constraint for uncalibrated cameras 라고 부른다.

Fundametal Matrix

아래의 식을 만족하는 행렬 FF가 fundamental matrix이다.
F=(K′)−⊤R′SbR′′⊤(K′′)−1\mathrm{F}=\left(\mathrm{K}^{\prime}\right)^{-\top} R^{\prime} \mathrm{S}_{b} R^{\prime \prime \top}\left(\mathrm{K}^{\prime \prime}\right)^{-1}
uncalibrated camera에서, 두 이미지 사이의 relative orientation에 관한 정보를 포함하는 행렬이다.

Projection Matrix에서 Fundamental Matrix 구하기

projection matrix를 왼쪽 3×33 \times 3 행렬, 오른쪽 3차원 벡터 형태로 나누어 표현한다.
P′=[A′∣a′]=[K′R′⏟A′∣−K′R′XO′⏟a′]\mathrm{P}^{\prime}=\left[\mathrm{A}^{\prime} \mid \mathbf{a}^{\prime}\right]=[\underbrace{\mathrm{K}^{\prime} \mathrm{R}^{\prime}}_{\mathrm{A}^{\prime}} \mid \underbrace{-\mathrm{K}^{\prime} \mathrm{R}^{\prime} \boldsymbol{X}_{O^{\prime}}}_{\mathbf{a}^{\prime}}]
위 식을 통해 XO′,XO′′\boldsymbol{X}_{O^{\prime}},\boldsymbol{X}_{O^{\prime\prime}} 을 구할 수 있다.
A′−1a′=(K′R′)−1a′=−R′⊤K′−1 K′R′XO′=−XO′\mathrm{A}^{\prime-1} \mathrm{a}^{\prime}=\left(\mathrm{K}^{\prime} \mathrm{R}^{\prime}\right)^{-1} \mathbf{a}^{\prime}=-\mathrm{R}^{\prime \top} \mathrm{K}^{\prime-1} \mathrm{~K}^{\prime} \mathrm{R}^{\prime} \boldsymbol{X}_{O^{\prime}}=-\boldsymbol{X}_{O^{\prime}}
XO′=−A′−1a′XO′′=−A′′−1a′′\boldsymbol{X}_{O^{\prime}}=-\mathrm{A}^{\prime-1} \mathbf{a}^{\prime} \\ \boldsymbol{X}_{O^{\prime\prime}}=-\mathrm{A}^{\prime\prime-1} \mathbf{a}^{\prime\prime}
또한 base line b12′\boldsymbol{b}_{12}^{\prime} 또한 위의 식을 이용해 구할 수 있다.
b12′=−A′′−1a′′+A′−1a′\boldsymbol{b}_{12}^{\prime}=-\mathrm{A}^{\prime \prime-1} \mathbf{a}^{\prime \prime}+\mathrm{A}^{\prime-1} \mathbf{a}^{\prime}
최종적으로 Fundamental Matrix를 A′,A′′\mathrm{A}^{\prime}, \mathrm{A}^{\prime\prime}을 이용해 나타내자.
F=(K′)−⊤R′SbR′′⊤(K′′)−1=A′−⊤Sb12′A′′−1\mathrm{F}=\left(\mathrm{K}^{\prime}\right)^{-\mathrm{\top}} R^{\prime} \mathrm{S}_{b} R^{\prime \prime \top}\left(\mathrm{K}^{\prime \prime}\right)^{-1}=\mathrm{A}^{\prime-\top} \mathrm{S}_{b_{12}^{\prime}} \mathrm{A}^{\prime \prime-1}

Coplanarity Constraint for Calibrated Cameras

•
Angle-Preserving 한 카메라를 가정한다
•
대부분의 카메라 시스템은 calibrated camera이다.
•
2개의 카메라가 같은 calibration matrix를 가진다고 가정한다
•
여기서는 distortion, error 가 존재하지 않는다고 가정한다.
x′=P′X′=K′R′[I3∣−XO′]X′=K′kx′\mathbf{x}^{\prime}=\mathrm{P}^{\prime} \mathbf{X}^{\prime}=\mathrm{K}^{\prime} R^{\prime}\left[I_{3} \mid-X_{O}^{\prime}\right] \mathbf{X}^{\prime}=\mathrm{K}^{\prime k} \mathbf{x}^{\prime}
위의 식을 살펴보면 주어진 이미지 평면상의 2차원 점은 3차원 world 좌표계를 카메라 좌표계로 translate, rotate한 값을 구한 후 calibration matrix를 곱한 것을 알 수 있다. 따라서 calibration 값을 곱하기 전이 바로 카메라의 방향을 의미하는 값임을 알 수있다.
calibration matrix에 기반하여, 우리는 direction을 얻을 수 있다.
앞서 소개한 fundamental matrix의 식 x′⊤Fx′′=0\mathrm{x}^{\prime \top} \mathrm{Fx}^{\prime \prime}=0 을 이용하면,
x′⊤(K′)−T(R′)−TSb(R′′)−1( K′′)−1⏟fundametal matrix Fx′′=0\mathrm{x}^{\prime \top} \underbrace{\left(\mathrm{K}^{\prime}\right)^{-\mathrm{T}}\left(R^{\prime}\right)^{-\mathrm{T}} S_{b}\left(R^{\prime \prime}\right)^{-1}\left(\mathrm{~K}^{\prime \prime}\right)^{-1}}_{\mathrm{fundametal \,matrix \, F}} \mathrm{x}^{\prime \prime}=0
x′⊤(K′)−T⏟kx′⊤R′SbR′′⊤(K′′)−1x′′⏟kx′′=0\underbrace{x^{\prime \top}\left(K^{\prime}\right)^{-T}}_{{ }^{k} \mathbf{x}^{\prime \top}} R^{\prime} S_{b} R^{\prime \prime \top} \underbrace{\left(K^{\prime \prime}\right)^{-1} \mathbf{x}^{\prime \prime}}_{{ }^{k} \mathbf{x}^{\prime \prime}}=0
kx′⊤R′SbR′′⊤⏟Ekx′′=0{ }^{k} \mathrm{x}^{\prime \top} \underbrace{R^{\prime} S_{b} R^{\prime \prime \top}}_{ \mathrm{E}} { }^{k}\mathbf{x}^{\prime \prime}= 0
kx′⊤E kx′′=0{ }^{k} \mathbf{x}^{\prime \top} \mathrm{E} \,{ }^{k} \mathbf{x}^{\prime \prime}=0

위와 같은 식을 coplanarity constraint for calibrated cameras 라고 부른다.

Essential Matrix

calibrated camera에 한정하여, 행렬 EE 를 essential matrix라고 한다.
E=R′SbR′′⊤\mathrm{E}=R^{\prime} \mathrm{S}_{b} R^{\prime \prime \top}
•
Essential Matrix는 5 degree of freedom을 가집니다.
•
calibrated camera에 해당하는 이미지 쌍의 relative orientation을 결정하는 5가지 파라미터가 존재합니다.
•
총 9개의 element(3×33 \times 3 행렬)중 5개를 제외한 4개의 constraints를 가집니다.
•
Essential Matrix는 homogeneous 좌표계에서 성립합니다
•
역행렬이 존재하지 않습니다 → rank deficiency를 갖는다!
Made with