Linear Algebra
///
///
📻

Camera Parameters: Extrinsic/Intrinsic

생성일
2022/01/28 04:41
태그
Calibration
DLT
Intrinsic
Extrinsic

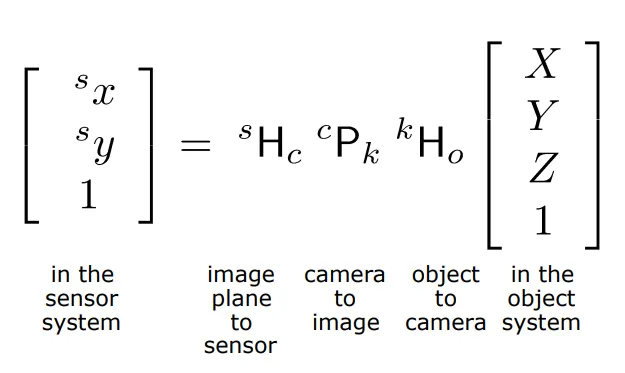
3차원 월드 좌표계의 한 점에서 카메라 2차원 센서 좌표계의 한 점으로 어떻게 매핑되는지 묘사해보자!

x=PX\mathbf{x}=\mathbf{P X}
[xy1]=P[XYZ1]\left[\begin{array}{l}x \\y \\1\end{array}\right]=\mathrm{P}\left[\begin{array}{l}X \\Y \\Z \\1\end{array}\right]

2D pixel coordinate(x\mathbf{x}) ← 3D world coordinate(X\mathbf{X})

Coordinate System의 종류

1.
World / object coordinate system [X,Y,Z]⊤[X, Y, Z]^{\top} (index가 없다는 건 object sys를 의미한다)
2.
Camera Coordinate System [kX,kY,kZ]⊤\left[{ }^{k} X,{ }^{k} Y,{ }^{k} Z\right]^{\top}
3.
Image Plane Coordinate System [cx,cy]⊤\left[{ }^{c} x,{ }^{c} y\right]^{\top}
4.
Sensor Coordinate System [sx,sy]⊤\left[{ }^{s} x,{ }^{s} y\right]^{\top}
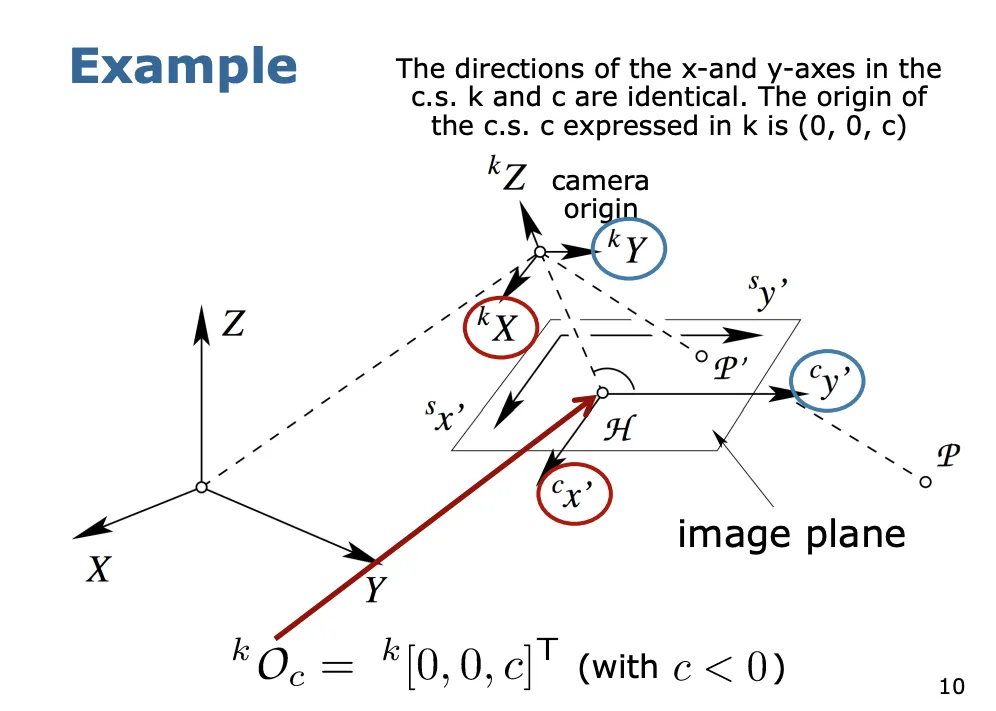
우리는 이제 system들간의 변환 관계에 대해서 살펴보게 될 것이다. 아래는 변환 과정을 시각적으로 묘사한 그림이다.

Transformation

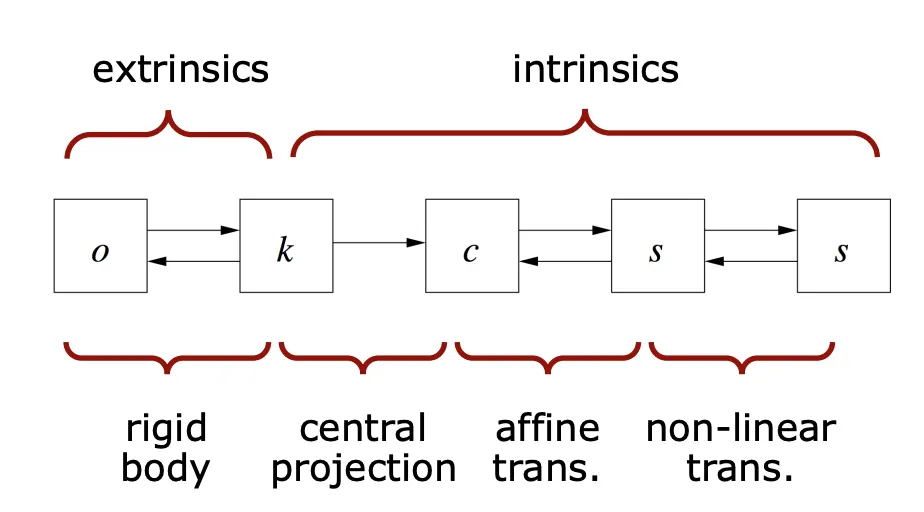
변환과정은 크게 4가지 단계로 나뉘어진다.

[1단계] Rigid body Transformation(World → Camera)

Extrinsic Parameters

카메라가 world 좌표계에서 어떤 위치와 방향(Pose)을 가지는 지를 설명하는 파라미터입니다.
•
총 6개의 파라미터가 필요합니다! (position : 3개 / Heading : 3개)
•
Invertible합니다!

Transformation

world coordinate 상의 점 P \mathcal{P}를 아래와 같이 정의한다.
XP=[XP,YP,ZP]⊤\boldsymbol{X}_{\mathcal{P}}=\left[X_{\mathcal{P}}, Y_{\mathcal{P}}, Z_{\mathcal{P}}\right]^{\top}
카메라 coordinate의 원점 O를 아래와 같이 정의한다.
XO=[XO,YO,ZO]⊤\boldsymbol{X}_{O}=\left[X_{O}, Y_{O}, Z_{O}\right]^{\top}
변환을 위해서는 Translation과 Rotation이 수반되고 이를 반영하는 식은 아래와 같다. 이것은 Euclidian coordinates에서 표현하는 방식이 된다.
kXP=R(XP−XO){ }^{k} \boldsymbol{X}_{\mathcal{P}}=R\left(\boldsymbol{X}_{\mathcal{P}}-\boldsymbol{X}_{O}\right)
Homogenous coordinates에서 표현해보면 아래와 같다.
[kXP1]=[R00⊤1][I3−XO0⊤1][XP1]=[R−RXO0⊤1][XP1]\begin{aligned}\left[\begin{array}{c}{ }^{k} \boldsymbol{X}_{\mathcal{P}} \\{1}\end{array}\right] &=\left[\begin{array}{cc}R & \mathbf{0} \\\mathbf{0}^{\top} & 1\end{array}\right]\left[\begin{array}{cc}I_{3} & -\boldsymbol{X}_{O} \\\mathbf{0}^{\top} & 1\end{array}\right]\left[\begin{array}{c}\boldsymbol{X}_{{\mathcal{P}}} \\1\end{array}\right] \\&=\left[\begin{array}{cc}R & -R \boldsymbol{X}_{O} \\\mathbf{0}^{\top} & 1\end{array}\right]\left[\begin{array}{c}\boldsymbol{X}_{\mathcal{P}} \\1\end{array}\right]\end{aligned}
따라서, world coordinates에서 카메라 coordinates으로 변환하는 행렬이 완성되었다.
kXP=kHXP with kH=[R−RXO0⊤1]{ }^{k} \mathbf{X}_{\mathcal{P}}={ }^{k} \mathrm{H} \mathbf{X}_{\mathcal{P}} \quad \text { with } \quad{ }^{k} \mathrm{H}=\left[\begin{array}{cc}R & -R \boldsymbol{X}_{O} \\\mathbf{0}^{\top} & 1\end{array}\right]

[2단계] Central Projection(Camera → Image)

Intrinsic Parameters

카메라 좌표계의 점에서 센서 좌표계의 점까지 투영하는 과정에서의 파라미터를 말하며, 카메라 앞의 scene과 이미지 평면 픽셀 간의 매핑을 나타냅니다.
•
Central Projection의 경우 Invertible하지 않지만, Image to Sensor, Model Deviation은 invertible합니다.

Ideal Perspective Projection

•
무왜곡 렌즈이다
•
모든 광선은 곧은 직선의 형태로 나타내며 Projection center를 통과한다. 이 점은 카메라 좌표계의 원점 SkS_k이다.
•
Focal point와 principal point H\mathcal{H} 가 optical axis(가로축)에 놓여 있다.
•
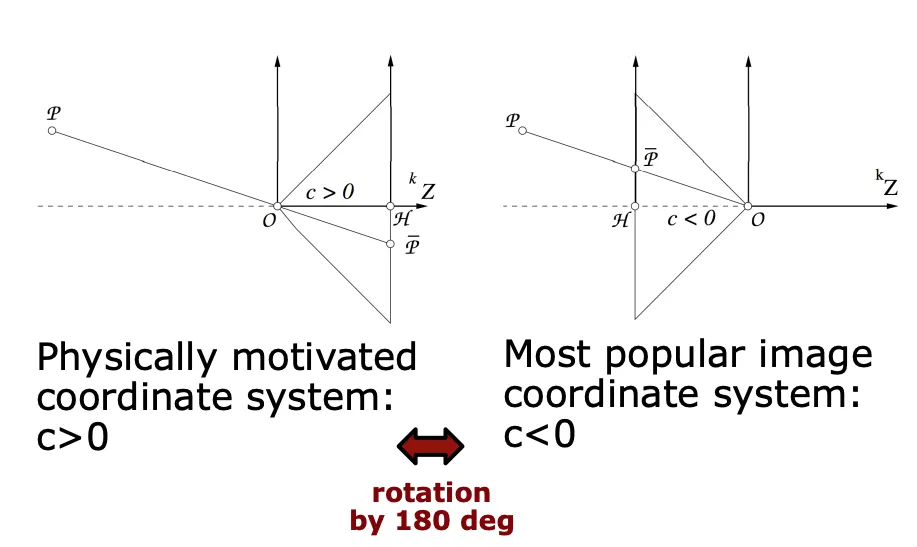
카메라 원점과 이미지 평면과의 거리를 cc 로 표현한다. (주로 cc < 0 으로 둔다, 그대로 두면 상이 반대로 맺히기 때문입니다) (Projection center OO 와 principal Point H\mathcal{H}의 거리 = focal length)
여기서 삼각형의 닮음 관계를 이용하여 이미지 평면에 투영된 점 P‾\overline{\mathcal{P}} 를 얻게 된다.
cxPˉ:=kXPˉ=ckXPkZPcyΦˉ:=kYPˉ=ckYPkZP(c=kZPˉ=ckZPkZP)\begin{array}{c}{ }^{c} x_{\bar{P}}:={ }^{k} X_{\bar{P}}=c \frac{{ }^{k} X_{\mathcal{P}}}{{ }^{k} Z_{P}} \\{ }^{c} y_{\bar{\Phi}}:={ }^{k} Y_{\bar{P}}=c \frac{{ }^{k} Y_{P}}{{ }^{k} Z_{P}} \\\left(c={ }^{k} Z_{\bar{P}}=c \frac{{ }^{k} Z_{\mathcal{P}}}{{ }^{k} Z_{P}}\right)\end{array}
Homogenous Coordinate에서 표현한다면
cxPˉ=[cxPˉcyP‾1]=[c0000c000010][kXPkYPkZP1]{ }^{c} \mathbf{x}_{\bar{P}}=\left[\begin{array}{c}{ }^{c} x_{\bar{P}} \\{ }^{c} y_{\overline{\mathcal{P}}} \\{ 1} \end{array}\right]=\left[\begin{array}{llll}c & 0 & 0 & 0 \\0 & c & 0 & 0 \\0 & 0 & 1 & 0\end{array}\right]\left[\begin{array}{c}{ }^{k} X_{\mathcal{P}} \\{ }^{k} Y_{\mathcal{P}} \\{ }^{k} Z_{\mathcal{P}} \\1\end{array}\right]
최종적인 world 좌표계에서 이미지 평면까지의 앞서 구한대로 변환 결과가 도출된다.
[ckXpkZpckYpkZp1]\left[\begin{array}{c}c \frac{{ }^{k} X_{p}}{{ }^{k} Z_{p}} \\c \frac{{ }^{k} Y_{p}}{{ }^{k} Z_{p}} \\1\end{array}\right]

Calibration Matrix

위의 결과를 기호로 모델링한다면 아래와 같다.
cxPˉ=cPkkXP{ }^{c} \mathbf{x}_{\bar{P}}={ }^{c} \mathrm{P}_{k}{ }^{k} \mathbf{X}_{\mathcal{P}}
cPk=[c0000c000010]{ }^{c} \mathrm{P}_{k}=\left[\begin{array}{cccc}c & 0 & 0 & 0 \\0 & c & 0 & 0 \\0 & 0 & 1 & 0\end{array}\right]
이런 상황에서 각 기호들을 묶어 조금 더 보기 직관적이게 표현한다면
cX=cPX{ }^{c} \mathbf{X}={ }^{c} \mathrm{P} \mathbf{X}
cP=cPkkH=[c0000c000010][R−RXO0⊤1]{ }^{c} \mathrm{P}={ }^{c}{ }^{} \mathrm{P}_{k}{ }^{k} \mathrm{H}=\left[\begin{array}{cccc}c & 0 & 0 & 0 \\0 & c & 0 & 0 \\0 & 0 & 1 & 0\end{array}\right]\left[\begin{array}{cc}R & -R \boldsymbol{X}_{O} \\\mathbf{0}^{\top} & 1\end{array}\right]
이 때, 우리는 새로운 이상적인 카메라 라는 가정하에 Calibration Matrix를 정의할 수 있다. (단, 이 경우는 ideal camera를 한정한다)
cK=[c000c0001]{ }^{c} \mathrm{K}=\left[\begin{array}{lll}c & 0 & 0 \\0 & c & 0 \\0 & 0 & 1\end{array}\right]
이 matrix를 이용해서 우리는 전체적인 mapping을 아래와 같이 표현 할 수 있다.
cP=cK[R∣−RXO]=cKR[I3∣−XO]{ }^{c} \mathrm{P}={}^{c} \mathrm{K}\left[R \mid-R \boldsymbol{X}_{O}\right]={ }^{c} \mathrm{K} R\left[I_{3} \mid-X_{O}\right]
따라서 우리는 world 좌표계의 한 점으로부터 이미지 평면으로 투영되는 점을 구하게 된다.
cx=cKR[I3∣−XO]X{ }^{c} \mathbf{x}={ }^{c} \mathrm{K} R\left[\boldsymbol{I}_{3} \mid-\boldsymbol{X}_{O}\right] \mathbf{X}
위 식을 행렬 꼴로 풀면 아래와 같다.
[cu′cv′cw′]=[c000c0001][r11r12r13r21r22r23r31r32r33][X−XOY−YOZ−ZO]\left[\begin{array}{l}{ }^{c} u^{\prime} \\{ }^{c} v^{\prime} \\{ }^{c} w^{\prime}\end{array}\right]=\left[\begin{array}{lll}c & 0 & 0 \\0 & c & 0 \\0 & 0 & 1\end{array}\right]\left[\begin{array}{lll}r_{11} & r_{12} & r_{13} \\r_{21} & r_{22} & r_{23} \\r_{31} & r_{32} & r_{33}\end{array}\right]\left[\begin{array}{c}X-X_{O} \\Y-Y_{O} \\Z-Z_{O}\end{array}\right]
마지막으로 실제 값을 구하기 위해 Euclidian Coordinates에서 표현하면 마무리 된다!
cx=cr11(X−XO)+r12(Y−YO)+r13(Z−ZO)r31(X−XO)+r32(Y−YO)+r33(Z−ZO){ }^{c} x=c \frac{r_{11}\left(X-X_{O}\right)+r_{12}\left(Y-Y_{O}\right)+r_{13}\left(Z-Z_{O}\right)}{r_{31}\left(X-X_{O}\right)+r_{32}\left(Y-Y_{O}\right)+r_{33}\left(Z-Z_{O}\right)}
cy=cr21(X−XO)+r22(Y−YO)+r23(Z−ZO)r31(X−XO)+r32(Y−YO)+r33(Z−ZO){ }^{c} y=c \frac{r_{21}\left(X-X_{O}\right)+r_{22}\left(Y-Y_{O}\right)+r_{23}\left(Z-Z_{O}\right)}{r_{31}\left(X-X_{O}\right)+r_{32}\left(Y-Y_{O}\right)+r_{33}\left(Z-Z_{O}\right)}

[3단계] Affine Transformation (Image → Sensor)

•
linear error만을 고려합니다, Non-linear Error는 고려하지 않습니다.
•
pixel coordinate로의 mapping이라고 부르기도 합니다.

Location of the Principal Point

sensor system의 원점이 image plane에서의 Principal point에 존재하지 않기 때문에 shift를 통해서 옮겨주어야 합니다.

Shear and Scale Difference

x와 y 사이의 Scale difference mm과 Shear compensation s를 추가해줍니다. (디지털 카메라에 한해서는 일반적으로 s≈0s \approx 0 으로 간주할 수 있습니다)
sHc=[1sxH01+myH001]{ }^{s} \mathrm{H}_{c}=\left[\begin{array}{ccc}1 & s & x_{H} \\0 & 1+m & y_{H} \\0 & 0 & 1\end{array}\right]
여기까지 구하면 우린 이제 Sensor 평면에서의 좌표를 얻을 수 있습니다!
sX=sHcc KR[I3∣−XO]X{ }^{s} \mathbf{X}={ }^{s} \mathrm{H}_{c}{ }^{c} \mathrm{~K} R\left[I_{3} \mid-\boldsymbol{X}_{O}\right] \mathbf{X}

Calibration Matrix

변환 sHc{ }^{s} \mathrm{H}_{c}는 Calibration matrix cK{ }^{c} \mathrm{K}와 결합하여 새로운 Calibration Matrix를 만듭니다.
이 Calibration matrix가 affine transformation 그 자체입니다.
K=sHccK=[1sxH01+myH001][c000c0001]=[ccsxH0c(1+m)yH001]\begin{aligned}\mathrm{K} & {=}^{s} \mathrm{H}_{c}{ }^{c} \mathrm{K} \\&=\left[\begin{array}{ccc}1 & s & x_{H} \\0 & 1+m & y_{H} \\0 & 0 & 1\end{array}\right]\left[\begin{array}{lll}c & 0 & 0 \\0 & c & 0 \\0 & 0 & 1\end{array}\right] \\&=\left[\begin{array}{ccc}c & c s & x_{H} \\0 & c(1+m) & y_{H} \\0 & 0 & 1\end{array}\right]\end{aligned} \\
정리하면, affine transformation은 5가지 파라미터를 포함합니다.
•
Camera constant: cc
•
principal point: xH,yHx_{H}, y_{H}
•
scale difference: mm
•
shear: ss

DLT : Direct Linear Transform (지금까지의 여정을 다 합치는 변환)

Object coordinate system에서부터 Sensor coordinate system까지의 변환과정을 의미한다. affine camera를 모델링 한 것입니다. 이 과정에서 우리는 총 11개의 파라미터를 얻게 된다. extrinsic parameters: R,XOR, \boldsymbol{X}_{O} (6개), intrinsic parameters: c,xH,yH,m,sc, x_{H}, y_{H}, m, s (5개) → 총 11개!
Homogeneous coordinate이 아닌 Euclidian space에서의 좌표를 표현하면 아래와 같다.

[4단계] Non-linear Error Correction (In Sensor)

•
이 단계에서 이전에 고려하지 않았던 non-linear error를 보정합니다!
•
non-linear error가 생기는 이유는 무엇일까요? → (1) 부정확한 렌즈 (2) 센서의 평면성 등등......

General Mapping

ax=sx+Δx(x,q)ay=sy+Δy(x,q)\begin{array}{l}{ }^{a} x={ }^{s} x+\Delta x\left(\boldsymbol{x}_{,} \boldsymbol{q}\right) \\{ }^{a} y={ }^{s} y+\Delta y(\boldsymbol{x} ,{\boldsymbol{q}})\end{array}
ax=aHs(x) sx{ }^{a} \mathbf{x}={ }^{a} \mathrm{H}_{s}(\boldsymbol{x})\,{ }^{s} \mathbf{x}
aHs(x)=[10Δx(x,q)01Δy(x,q)001]{ }^{a} \mathrm{H}_{s}(\boldsymbol{x})=\left[\begin{array}{ccc}1 & 0 & \Delta x(\boldsymbol{x}, \boldsymbol{q}) \\0 & 1 & \Delta y(\boldsymbol{x}, \boldsymbol{q}) \\0 & 0 & 1\end{array}\right]
따라서 전체적인 mapping은 다음과 같다.
ax=aHs(x)KR[I3∣−XO]X{ }^{a} \mathbf{x}={ }^{a} \mathrm{H}_{s}(\boldsymbol{x}) \mathrm{K} R\left[I_{3} \mid-\boldsymbol{X}_{O}\right] \mathbf{X}
이렇게 non-linear errors까지 보정을 하고 나면 아래와 같은 결과를 얻을 수 있다.

General Calibration Matrix

General Calibration Matrix는 하나의 affine camera와 general mapping을 결합 한다.
aK(x,q)=aHs(x,q)K=[ccsxH+Δx(x,q)0c(1+m)yH+Δy(x,q)001]\begin{aligned}{ }^{a} \mathrm{K}(\boldsymbol{x}, \boldsymbol{q}) &={ }^{a} \mathrm{H}_{s}(\boldsymbol{x}, \boldsymbol{q}) \mathrm{K} \\&=\left[\begin{array}{ccc}c & c s & x_{H}+\Delta x(\boldsymbol{x}, \boldsymbol{q}) \\0 & c(1+m) & y_{H}+\Delta y(\boldsymbol{x}, \boldsymbol{q}) \\0 & 0 & 1\end{array}\right]\end{aligned}
따라서 최종적인 general camera model이 완성된다 (진짜 끝판대장)
ax=aP(x,q)X{ }^{a} \mathbf{x}={ }^{a} \mathrm{P}(\boldsymbol{x}, \boldsymbol{q}) \mathbf{X}
aP(x,q)=aK(x,q)R[I∣−XO]{ }^{a} \mathrm{P}(\boldsymbol{x}, \boldsymbol{q})={ }^{a} \mathrm{K}(\boldsymbol{x}, \boldsymbol{q}) R\left[\boldsymbol{I} \mid-\boldsymbol{X}_{O}\right]
distortion은 따로 포스트를 할애해 작성해 보도록 하겠습니다.

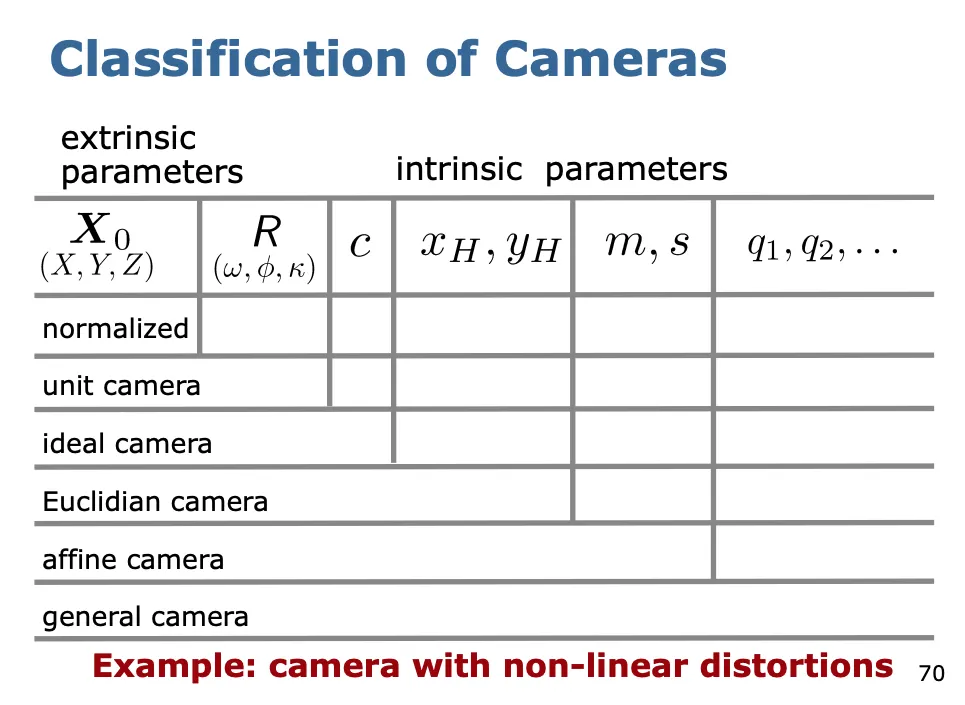
카메라 분류하기

Calibrated Camera 정의하기

•
intrinsic 파라미터를 모른다면, 우리는 카메라가 uncalibrated 되었다고 부릅니다.
•
intrinsic 파라미터를 안다면, 우리는 카메라가 calibrated 되었다고 부릅니다.
•
intrinsic 파라미터를 얻는 과정이 바로 camera calibration입니다.
•
만약 intrinsic 파라미터를 알고 그 값이 변하지 않는다면, 우리는 이러한 카메라를 metric camera라고 부릅니다.
Made with