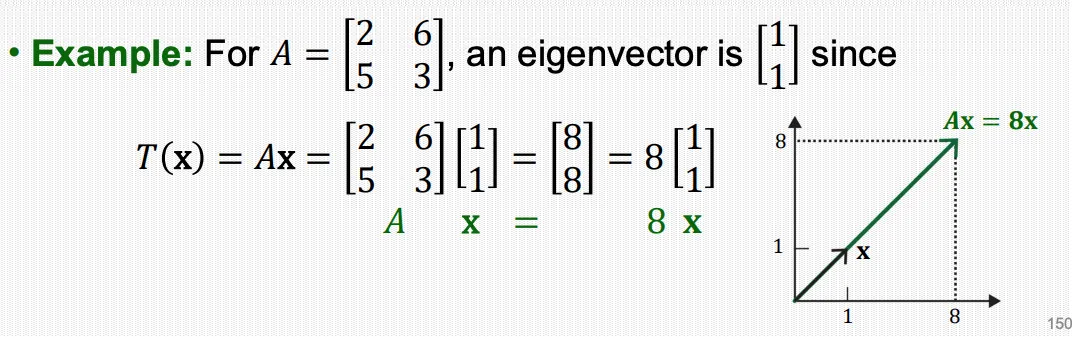Linear Algebra
///
///
🚓

3. Eigenvalue Decomposition

태그
Eigenvector
Eigenvalue
Diagonalization
EVD

Eigenvectors and Eigenvalues

square matrix A∈Rn×nA \in \mathbb{R}^{n \times n} 의 eigenvector는 임의의 스칼라 값 λ\lambda에 대해 Ax=λxA \mathbf{x}=\lambda \mathbf{x}를 만족하는 0이 아닌 벡터 x∈Rn\mathbf{x} \in \mathbb{R}^{n}이다. 또한 λ\lambda 값이 eigenvalue가 된다.
Eigenvectors 와 Eigenvalues는 서로 연관되어 있다.
위 예제를 살펴보면, 주어진 벡터 x\mathbf{x}가 eigenvector일 때, 변환을 행하는 AxA\mathbf{x} 의 결과값이 벡터 x\mathbf{x} 의 방향과 동일하고 크기만 다르다는 것을 알 수 있다.
이러한 방법으로 계산하는 경우 계산 속도가 현저히 빠르다는 것을 알수 있다. (행렬계산으로 하는 것보단 스칼라 값으로 계산하는 것이 훨씬 빠르니까 ^^;)

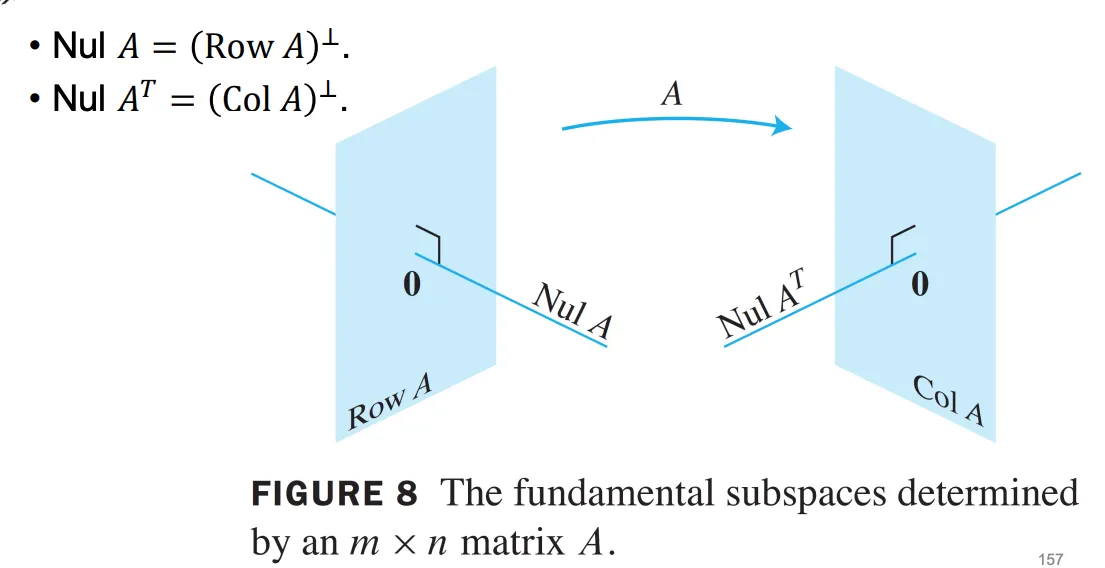
Null space

행렬 A∈Rm×nA \in \mathbb{R}^{m \times n}에 대해 Ax=0A \mathbf{x}=\mathbf{0} 를 만족하는 모든 해의 집합을 말하며,  Nul A\text { Nul } A 라고 표기한다. 이 때 백터 x\mathbf{x}는 반드시 모든 row vector와 orthogonal 해야 한다.
임의의 행렬 A=[a1⊤a2⊤⋮am⊤]A=\left[\begin{array}{c}\mathbf{a}_{1}^{\top} \\\mathbf{a}_{2}^{\top} \\\vdots \\\mathbf{a}_{m}^{\top}\end{array}\right]에 대해 , 아래 조건을 만족한다.
a1⊤x=0,a2⊤x=0,…,am⊤x=0\mathbf{a}_{1}^{\top} \mathbf{x}=0, \mathbf{a}_{2}^{\top} \mathbf{x}=0, \ldots, \mathbf{a}_{m}^{\top} \mathbf{x}=0

Orthogonal Complement

백터 z\mathbf{z}가 subspace WW 의 모든 벡터와 orthogonal 하다면, 그러한 벡터 z\mathbf{z}의 성질을 만족하는 집합을 WW의 orthogonal complement라고 하고 W⊥W^{\perp}라고 작성한다.

Characteristic Equation

그렇다면 이러한 eigenvalue를 찾기 위해서는 어떻게 해야 할까? 이런 경우 사용하는 것이 바로 특성 방정식이다. 아래와 같이 서술한다.
det⁡(A−λI)=0\operatorname{det}(A-\lambda I)=0

어떻게 determinant로 eigenvalue를 찾을 수 있을까?

(A−λI)x=0(A-\lambda I) \mathbf{x}=\mathbf{0}를 만족하는 0이 아닌 nontrivial solution을 찾기 위해서는 (A−λI)(A-\lambda I)를 구성하는 column vector들이 서로 linearly dependent 해야 하고, 그러기 위해서는 non-invertible해야 한다. 즉, 역행렬이 존재해서는 안되기 때문에, 자연스럽게 determinant 값도 0을 만족해야 한다.

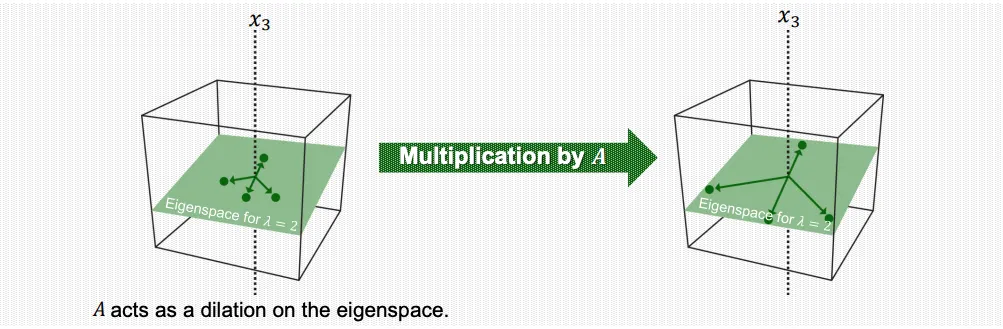
Eigenspace

앞서 제시한 수식을 정리하면, (A−λI)x=0(A-\lambda I) \mathbf{x}=\mathbf{0} 로 표현 할 수 있으며, 이 때 0을 제외한 해를 찾아야 하므로, nontrivial solution을 찾게 된다. 따라서 행렬 (A−λI)(A-\lambda I)의 null space를 eigenvalue λ\lambda에 대한 eigenspace라고 한다.(이 때, eigenspace에는 벡터 0\mathbf{0} 또한 포함된다.)
eigenvalue는 유일하지만, eigenvector는 무수히 많다. (다양한 조합으로 표현가능, 단 span은 동일) 이러한 eigenvector들이 형성하는 subspace가 eigenspace가 된다.

Diagonalization

square matrix A∈Rn×nA \in \mathbb{R}^{n \times n}가 주어졌을 때, 이 행렬을 diagonal matrix 형태로 표현하고 싶을 때, 아래와 같이 분해하는 것을 diagonalization이라고 한다.
D=V−1AVD=V^{-1} A V
이 때, V∈Rn×nV \in \mathbb{R}^{n \times n}는 invertible matrix이며, D∈Rn×nD \in \mathbb{R}^{n \times n}는 diagonal matrix를 의미한다.

Diagonalization이 가능하려면?

위의 식을 보면 알수 있겠지만, square matrix가 주어진다고 항상 diagonalize 할수 있는 것은 아니다. VV가 역행렬이 존재해야만 대각화가 가능하다. 다시 말하면,
•
행렬 V∈Rn×nV \in \mathbb{R}^{n \times n} 를 만족하는 square matrix이다.
•
행렬 VV를 구성하는 eigenvector(=column vector of VV)들이 linearly independent 해야 한다.
•
헷갈리지 말자! 일반행렬은 고유벡터들이 선형독립! 대칭행렬은 고유벡터들이 직교한다!

Eigendecomposition

행렬 AA가 diagonalizable하다면, D=V−1AVD=V^{-1} A V 로 작성할 수 있고, VV의 역행렬이 존재하기 때문에 수식을 전개하면 아래와 같이 서술 할 수 있다.
A=VDV−1A=V D V^{-1}
결국 diagonalizable하다는 것은 eigendecomposition이 가능하다는 것과 같은 말이다.

Linear Transformation via Eigendecomposition

임의의 벡터 x\mathbf{x}가 주어졌을 때에는 연산을 어떻게 해야 할까? 이러한 경우에는 벡터 x\mathbf{x}가 eigenvector가 아니기 때문에 Ax=λxA \mathbf{x}=\lambda \mathbf{x}가 성립하지 않기 때문에 앞서 언급한 계산 속도의 이점을 누릴 수 없다. 이 때 우리가 이전 포스트에서 언급했던 linearity의 성질을 떠올려본다면 주어진 벡터 x\mathbf{x}를 eigenvector의 linear combination의 형태로 표현할 수 있다. 이렇게 되면 Ax=λxA \mathbf{x}=\lambda \mathbf{x}의 성질을 이용하여 따로 따로 값을 구한후 더하면 된다. 계산 속도가 향상될 수 있다!
이를 수식적으로 표현하면 아래와 같이 서술한다.
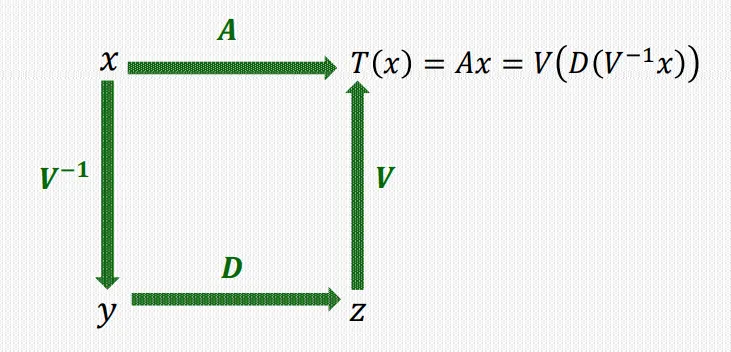
행렬 AA가 diagonalizable하다면, A=VDV−1A=V D V^{-1}의 형태로 eigendecomposition 가능하고, 이를 통해 linear Transformation T(x)=AxT(\mathbf{x})=A \mathbf{x}를 생각해 볼 수 있다.
T(x)=Ax=VDV−1x=V(D(V−1x))T(\mathbf{x})=A \mathbf{x}=V D V^{-1} \mathbf{x}=V\left(D\left(V^{-1} \mathbf{x}\right)\right)
총 3단계의 연속적인 변환으로 해석하게 된다. 임의로 주어진 백터 x\mathbf{x}를 eigenvector들의 linear combination으로 표현하고 이를 이용해 쉬운 식으로 치환하고 계산한 후 다시 복원하는 형태를 띈다.

1단계. Basis 바꾸기 (V−1x)(V^{-1} \mathbf{x})

주어진 벡터 x\mathbf{x}를 eigenvector를 basis로 하는 linear combination으로 표현한다. 이를 위해 각 basis에 대한 coefficient를 구해야 한다. eigenvector로 이루어진 변환행렬을 VV로 두고, 각 column에 대한 coefficient vector를 y\mathbf{y}라고 한다면, 아래와 같이 서술할 수 있다.
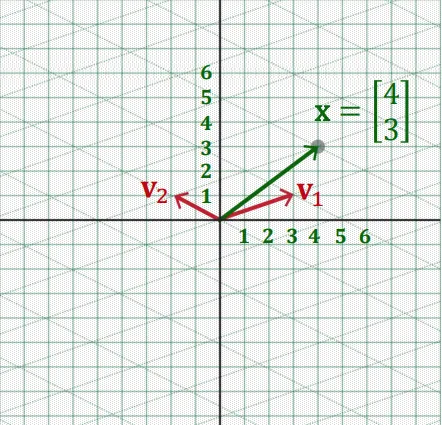
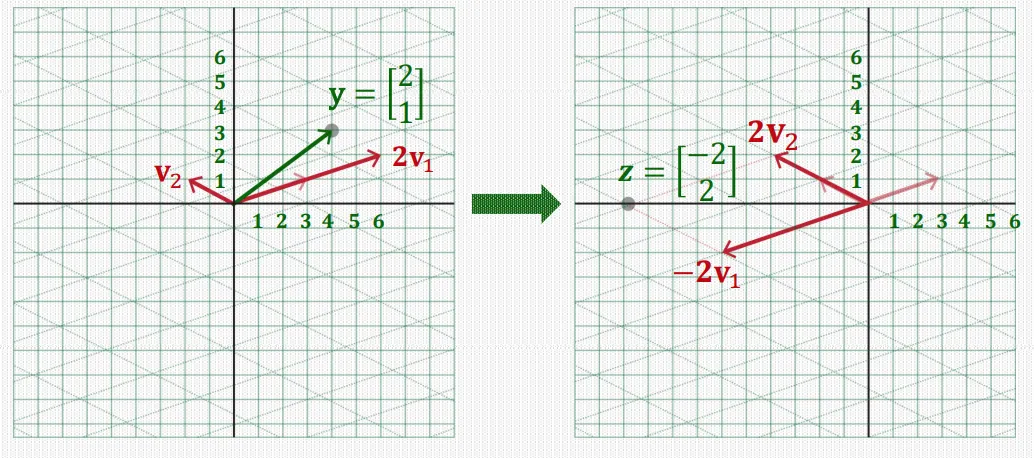
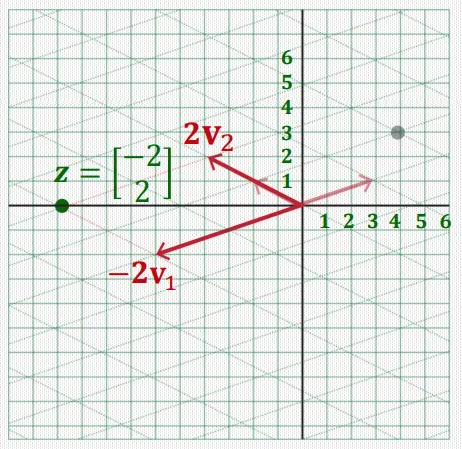
Vy=xy=V−1xV \mathbf{y}=\mathbf{x} \\ \mathbf{y} = V^{-1}\mathbf{x}
이해하기 쉽게 그림으로 제시하면 다음과 같다. 각 eigenvalue, eigenvector의 관계가 아래와 같다고 가정한다.
Av1=−1v1 and Av2=2v2A \mathbf{v}_{1}=-1 \mathbf{v}_{1} \text { and } A \mathbf{v}_{2}=2 \mathbf{v}_{2}
주어진 벡터 x\mathbf{x}는 원래 standard basis의 linear combination으로 이루어져 있었지만,
x=[43]=4[10]+3[01]=[1001][43]\mathbf{x}=\left[\begin{array}{l}4 \\3\end{array}\right]=4\left[\begin{array}{l}1 \\0\end{array}\right]+3\left[\begin{array}{l}0 \\1\end{array}\right]=\left[\begin{array}{ll}1 & 0 \\0 & 1\end{array}\right]\left[\begin{array}{l}4 \\3\end{array}\right]
eigenvector {v1,v2}\left\{\mathbf{v}_{1}, \mathbf{v}_{2}\right\} 로 이루어진 새로운 basis를 이용해 표현할 수 있고, 이때 각 eigenvector에 대한 coefficient vector y\mathbf{y}로 나타낼 수 있다.
x=Py=[v1v2][y1y2]=2v1+1v2⇒y=[21]\mathbf{x} = P \mathbf{y}=\left[\begin{array}{ll}\mathbf{v}_{1} & \mathbf{v}_{2}\end{array}\right]\left[\begin{array}{l}y_{1} \\y_{2}\end{array}\right]=2 \mathbf{v}_{1}+1 \mathbf{v}_{2} \Rightarrow \mathbf{y}=\left[\begin{array}{l}2 \\1\end{array}\right]

2단계. Element-wise Scaling (D(V−1x))\left(D\left(V^{-1} \mathbf{x}\right)\right)

Av1=−1v1 and Av2=2v2A \mathbf{v}_{1}=-1 \mathbf{v}_{1} \text { and } A \mathbf{v}_{2}=2 \mathbf{v}_{2}를 이용해 계산량을 줄이는 과정이다. 주어진 행렬곱을 스칼라와 벡터 곱으로 바꾼다.
z=Dy=[−1002][21]=[(−1)×22×1]=[−22]\mathbf{z}=D \mathbf{y}=\left[\begin{array}{cc}-1 & 0 \\0 & 2\end{array}\right]\left[\begin{array}{l}2 \\1\end{array}\right]=\left[\begin{array}{c}(-1) \times 2 \\2 \times 1\end{array}\right]=\left[\begin{array}{c}-2 \\2\end{array}\right]

3단계. 원래 Basis로 복귀하기 V(D(V−1x))V\left(D\left(V^{-1} \mathbf{x}\right)\right)

다시 standard basis의 형태로 구하기 위해 eigenvector를 각각 곱해주고 더하면 된다.
Vz=[v1v2][z1z2]=v1z1+v2z2Vz=\left[\begin{array}{ll}\mathbf{v}_{1} & \mathbf{v}_{2}\end{array}\right]\left[\begin{array}{l}z_{1} \\z_{2}\end{array}\right]=\mathbf{v}_{1} z_{1}+\mathbf{v}_{2} z_{2}
T(x)=V=[v1v2][−22]=−2v1+2v2=−2[31]+2[−21]=[−100]\begin{aligned} T(\mathbf{x})=V &=\left[\begin{array}{ll}\mathbf{v}_{1} & \mathbf{v}_{2}\end{array}\right]\left[\begin{array}{c}-2 \\2\end{array}\right] \\&=-2 \mathbf{v}_{1}+2 \mathbf{v}_{2} \\&=-2\left[\begin{array}{l}3 \\1\end{array}\right]+2\left[\begin{array}{c}-2 \\1\end{array}\right] \\&=\left[\begin{array}{c}-10 \\0\end{array}\right]\end{aligned}

위에서 제시한 transformation과정을 그림으로 표현하면 아래와 같다.

Linear Transformation via AkA^{k}

연속해서 행렬을 곱하는 상황 A×A×⋯×Ax=AkxA \times A \times \cdots \times A \mathbf{x}=A^{k} \mathbf{x} 을 생각해보면, 만약 행렬 AA가 diagonalizable하다면 아래와 같이 치환해 곱셈을 구할 수 있다.
A=VDV−1Ak=(VDV−1)(VDV−1)⋯(VDV−1)=VDkV−1A=V D V^{-1} \\ A^{k}=\left(V D V^{-1}\right)\left(V D V^{-1}\right) \cdots\left(V D V^{-1}\right)=V D^{k} V^{-1}
이 때 DkD^{k}는 간단히 계산될 수 있다.
Dk=[λ1k0⋯00λ2k⋱⋮⋮⋱⋱00⋯0λnk]D^{k}=\left[\begin{array}{cccc}\lambda_{1}^{k} & 0 & \cdots & 0 \\0 & \lambda_{2}^{k} & \ddots & \vdots \\\vdots & \ddots & \ddots & 0 \\0 & \cdots & 0 & \lambda_{n}^{k}\end{array}\right]
eigendecomposition V(Dk(V−1x))V\left(D^{k}\left(V^{-1} \mathbf{x}\right)\right)를 이용해 계산하게 되면 AkxA^{k}\mathbf{x} 를 직접 구하는 것 보다 훨씬 빠르게 행렬 곱셈을 수행할 수 있게 된다!

Eigenvalue, Diagonalization의 중요한 성질들

•
triangular matrix의 main diagonal의 요소들은 eigenvalue가 된다.
•
만약 v1,⋅⋅⋅,vr\mathbf{v_1},\cdot\cdot\cdot, \mathbf{v_r}가 n×n{n \times n} 행렬 AA의 distinct eigenvalues λ1,⋅⋅⋅,λr\lambda_1,\cdot\cdot\cdot, \lambda_r에 대응하는 eigenvector라면, 집합 {v1,⋅⋅⋅,vr}\left\{\mathbf{v_1},\cdot\cdot\cdot, \mathbf{v_r}\right\}은 linearly independent하다.
•
행렬 AA가 n개의 linearly independent eigenvector를 가지면 diagonalizable 합니다.
•
n×n{n \times n} 행렬이 n개의 distinct한(서로 다른) eigenvalue를 가지면 diagonalizable 합니다.

임의의 행렬 Diagonalize 해보기

Reference

인공지능을 위한 선형대수 강좌소개 : edwith
인공지능을 위한 선형대수
https://www.edwith.org/ai251
Made with