dive into deep learning

Chapter 4. Multi-Layer Perceptron

슬램과 함께 춤을

Deep Learning

dive into deep learning

Chapter 4. Multi-Layer Perceptron

🚚

Chapter 4. Multi-Layer Perceptron

생성일

2022/01/19 13:48

태그

MLP

Overfitting

Weight Decay

Dropout

4.1 Multilayer Perceptrons

앞선 단원에서 우리는 선형 모델을 살펴보았습니다.

\hat{\mathbf{o}}=\operatorname{softmax}(\mathbf{W} \mathbf{x}+\mathbf{b})

위와 같은 형태로 표현해 주어진 데이터가 어느 카테고리에 위치하는지 선형함수의 형태로 주어졌습니다. 그러나 이러한 선형함수는 입력들이 바로 출력으로 매핑되고 이는 너무 강한 가정입니다. 마치 넌 A형이니까~ 소심하겠지 뭐~ 라고 바로 단언해버리는 것과 같습니다. 세상 사람들이 다 제각각이듯이 하나의 특징을 통해 바로 하나의 결론으로 매듭짓기엔 너무 논리의 비약이 큽니다.

이러한 추론을 방지하기 위해선 우린 여러 요소들을 복합적으로 고려해야 합니다.

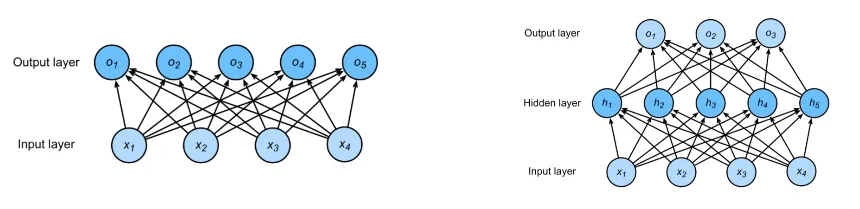
입력과 출력 사이의 복잡한 관계를 찾기 위해선 패턴 형성에 관여하는 수많은 특성들을 고려해야하고 이를 위해서 우리는 여러개의 hidden layers를 사용하여 모델을 구성하게 됩니다. 각 layer의 결과는 다음 layer의 입력으로 연결되고 차례 차례 이어져서 출력층까지 이어집니다. 이러한 아키텍쳐를 Multilayer Perceptron이라고 합니다. 이러한 Multilayer Perceptron은 여러 개의 layers의 뉴런들이 서로 Fully Connected된 형태를 가집니다.

이러한 복잡한 모델을 다루기 시작하면서 등장하는 문제들이 바로 overfitting, underfitting입니다. 위의 문제점들을 해결하기 위해 weight decay, dropout 등의 regularization techniques을 이용합니다. 또한 네트워크를 성공적으로 트레이닝 시키기 위한 numerical stability 와 parameter initialization을 다룬다.

4.1.1 Hidden Layers

위에 제시된 형태에서 기본적인 정보를 표현하면, 입력이 4개, 출력이 3개, 1개의 hidden layer가 5개의 hidden unit을 가지는 형태입니다. 층의 개수는 입력층을 제외한 2개입니다.

4.1.2 Activation Functions

\begin{aligned}&\mathbf{h}=\sigma\left(\mathbf{W}_{1} \mathbf{x}+\mathbf{b}_{1}\right) \\&\mathbf{o}=\mathbf{W}_{2} \mathbf{h}+\mathbf{b}_{2} \\&\hat{\mathbf{y}}=\operatorname{softmax}(\mathbf{o})\end{aligned}

Activation function은 입력된 데이터의 가중 합을 출력 신호로 변환하는 함수이다. 인공 신경망에서 이전 레이어에 대한 가중 합의 크기에 따라 활성 여부가 결정됩니다. 이러한 Activation function을 사용할 때 주로 비선형 함수를 사용합니다. 그 이유는 선형함수를 Activation function으로 사용하면 층을 깊게 하는 의미가 없이 그냥 선형함수가 되어 버리기 때문입니다. y(x)=h(h(h(x)))라는 식에서 h(x) = cx 라고 가정하면

y(x) = c^3(x)

의 선형함수가 되어 버린다.

그렇다면 Activation function에는 어떤 종류가 있을까?

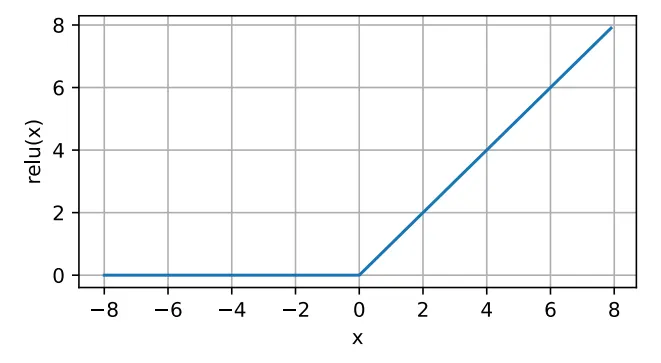
ReLU Function (most frequently used)

가장 구현하기 단순한 형태를 가지고 있고 퍼포먼스 또한 좋기 때문에 가장 많이 사용되는 함수이다. ReLU를 사용하는 가장 큰 이유는 기울기 값이 0이상의 입력에 대해서 1이기 때문에 기울기 값이 사라지지 않고 계속 유지되기 때문에 뒤에 후술할 Gradient Vanishing 문제에 대해 자유롭다.

\operatorname{ReLU}(x)=\max (x, 0)

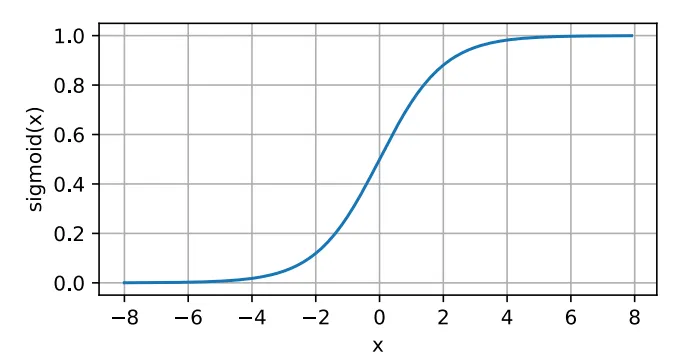
Sigmoid Function

어떠한 입력을 넣든 (0,1) 사이의 값으로 변환해 주는 함수이다. Sigmoid는 매우 매끄러운 형태의 곡선으로 기울기가 급격하게 변하지 않기 때문에 Gradient Exploding 현상이 발생하지는 않지만, 대부분의 입력에 대해 기울기가 0인 값을 가지기 때문에 앞 노드의 값이 어떤 값이었는지 상관 없이 기울기가 소멸해버리는 Gradient Vanishing 현상이 발생한다. 즉, 다음 layer에 아무 것도 전달되지 않는 현상이 발생해 신호가 전달되지 않는다.

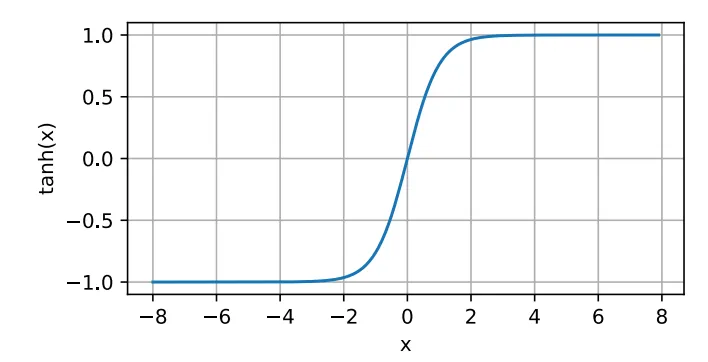
\operatorname{sigmoid}(x)=\frac{1}{1+\exp (-x)}

Tanh Function

\tanh (x)=\frac{1-\exp (-2 x)}{1+\exp (-2 x)}

4.4 Model Selection, Underfitting, and Overfitting

딥러닝을 포함한 머신러닝 알고리즘에서 가장 중요한 것은 패턴을 찾는것입니다.

하지만 우리는 단순히 패턴을 기억하는 것이 아닌 처음보는 유형에 대해서도 대응할 수 있는 알고리즘을 만들어야 합니다. 특정 상황에서만 사용되는 모델은 사용할 수 없고, 전혀 보지 못한 것에 예측 할 수 있어야 합니다. 따라서 일반적인 패턴을 찾는것이 가장 중요합니다.

하지만 우리가 접근하는 데이터의 양은 전체 데이터 양의 작은 일부분일 뿐입니다. 따라서 올바른 예측을 하기가 어렵고, 모델이 실제 분포보다 Training dataset 분포에만 더 근접하게 되는 현상이 발생하게 되며, 이를 Overfitting이라고 합니다.

4.4.1 Training Error and Generalization Error

Overfitting에 대해 본격적으로 다루기 전에, 우리는 2가지 형태의 Error가 존재함을 인지해야 합니다.

(1) Training Error → Training Dataset을 활용해 학습을 할때 생기는 Error (2) Generalization Error → 주어진 dataset이 아닌 다른 추가적인 dataset에 대한 Error

쉽게 말해 Training Error는 주어진 문제집을 가지고 어느정도 틀렸는지를 말한다면, Generalization Error는 생전 처음보는 시험문제를 가지고 비교하는 것입니다.

그렇다면 이러한 Generalizablity에 영향을 주는 요소에는 어떤것이 있을까요?

튜닝이 가능한 파라미터들의 개수 → 파라미터들의 개수가 많아질수록 오버피팅에 취약해 집니다.

파라미터가 가질수 있는 값의 범위 → weight의 범위가 클수록 오버피팅에 취약해 집니다.

Training Examples 개수 → 데이터의 수가 적다면 오버피팅에 취약해 집니다.

4.4.2 Model Selection

우리는 여러 모델들의 성능을 평가해서 모델을 선정해야합니다.

multilayer perceptron을 예로 들면, 우리가 컨트롤 할수 있는 부분들은 hidden layer의 개수, hidden unit의 개수, 각 hidden layer의 activation function를 선택할 수 있습니다. 모델을 선택하기 위한 성능평가 요소로 필요한 것이 바로 validation data set입니다. 그렇다면 왜 이러한 데이터셋이 필요할까요?

Model Selection 과정에서는 Test dataset을 사용해선 안되고, 그렇다고 Training data만을 사용하면 올바른 결과를 얻을 수 없습니다. 그 이유는 Generalization Error이 Training Error로 예상될 수 없기 때문입니다. 학교에서 시험을 보는데 지금까지 풀었던 문제랑 완전 똑같이 낼께~ 라고 말씀하시는 것과 같습니다. 이렇게 되면 그 친구가 진짜 알아서 푸는건지 아니면 그대로 외워서 푸는것인지 구분할수 없게 됩니다. 이를 고려해서, Training data와 Test dataset 이외의 데이터를 확보해서 모델 선택에 사용해야합니다. 이렇게 확보한 데이터가 validation data set이 됩니다. (6/9월 모의고사 같은 느낌(?))

데이터를 나눌 때는 Training data에서 임의로 선택한 일부의 데이터를 validation data set으로 사용하고, 나머지를 Training data로 사용하는 것이 정석입니다. (하지만 데이터가 부족하다면 이야기가 달라진다....)

K-fold Cross-Validation

앞서 말했듯 데이터가 완전 충분한 상황은 없다. 이러한 경우에는 부족한 데이터셋을 가지고 학습을 효율적으로 진행하기 위해 K-fold Cross-Validation을 이용한다. Original training data를 K개의 겹치지 않는 부분들로 나눈 뒤 모델 training / validation을 K번 수행한다.

https://kr.mathworks.com/discovery/cross-validation.html

한 번의 학습 때마다 (k-1)개의 subset으로 학습을 하고, 나머지 하나로 validation을 수행한다. 마지막으로 training / validation error 가 각 학습 때마다 나오면 값들을 평균 내어 전체 training / validation error를 구한다.

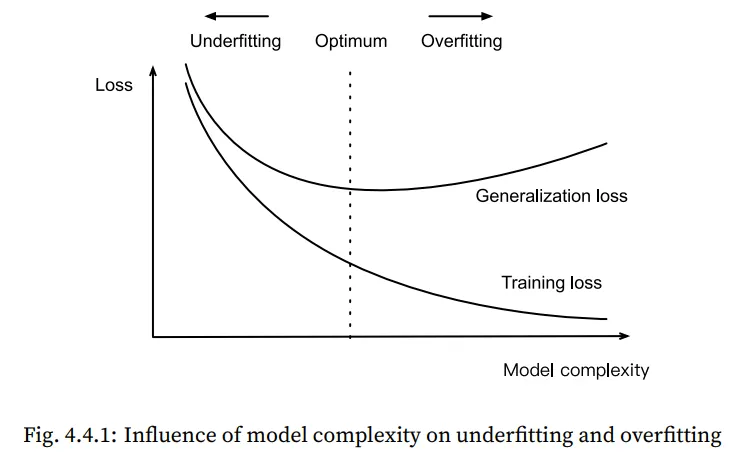
4.4.3 Underfitting or Overfitting?

Underfitting은 모델이 너무 간단하기 때문에 Training Error가 줄어들지 않는 것입니다. Overfitting은 앞에서 언급했듯이, Training Error가 Test dataset에 의한 Error보다 아주 작은 경우입니다.

이 두가지 경우는 반드시 모두 해결이 되어야 하며, 이를 해결하기 위해선 왜 이런 현상이 일어나는지 알아보아야 합니다.

Underfitting 과 Overfitting이 발생하는 가장 근본적인 원인 2가지를 뽑자면, 바로 모델의 Complexity와 데이터셋의 Size입니다.

1. Complexity(모델의 복잡도)

높은 차수의 다항식은 낮은 차수의 다항식보다 복잡하고 , 그렇기 때문에 더 많은 파라미터와 함수 선택의 범위가 넓습니다. 따라서 동일한 양의 Training Dataset을 가정했을 때, 고차 다항식이 더 낮은 Training Error를 가지게 됩니다. 하지만 주어진 데이터 대비 함수의 차수가 너무 높다면 Generalization Loss가 증가하게 됩니다.

따라서 적절한 Complexity를 설정해야만 Underfitting 과 Overfitting 문제를 해결할 수 있습니다.

2. Dataset Size(데이터셋의 크기)

모델을 고정시켜놓고, Training Dataset을 적으면 적을수록 Overfitting의 위험성은 높아집니다. 반대로 Training data를 늘리면 늘릴수록, Generalization Error는 감소합니다. 결과적으로 말하면, 데이터는 많을수록 좋습니다! 딥러닝의 성공은 다양한 매체를 통해 수많은 데이터셋을 이용하여 학습을 시켰기 때문에 가능해 졌습니다.

4.4.4 Polynomial Regression

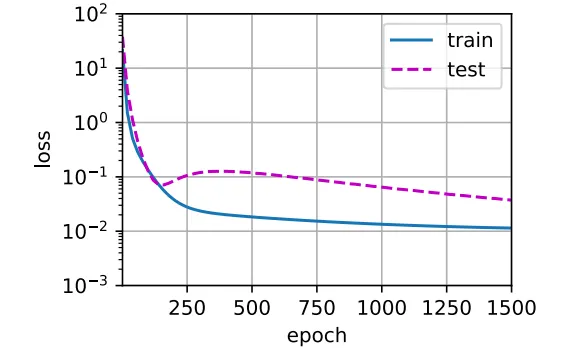
위에 제시한 Underfitting or Overfitting 상황을 만들어 실제 함수에서 training loss가 어떠한 상황에 처해지는지 확인해보자.

y=5+1.2 x-3.4 \frac{x^{2}}{2 !}+5.6 \frac{x^{3}}{3 !}+\epsilon \text { where } \epsilon \sim \mathcal{N}\left(0,0.1^{2}\right)

위 처럼 주어진 임의의 3차 다항식을 이용해 데이터를 만들어봅니다, 이 때 실제 데이터로 묘사하기 위해 ε항을 추가하고 이는 평균이 0이고 분산이 (0.1)^2 인 분포입니다. 상식적으로 생각하였을 때 위 식을 가장 잘 묘사할수 있는 다항식은 3차 다항식인것을 당연히 알수 있지만, 실제 상황에서는 위와 같은 식이 주어지지도 않을 뿐더러 outlier들도 많기 때문에 다항식의 차수를 짐작하기란 쉽지 않습니다.

이러한 상황에서 우리는 여러가지 차수로 함수를 가정하고 학습을 시켜보도록 하겠습니다.

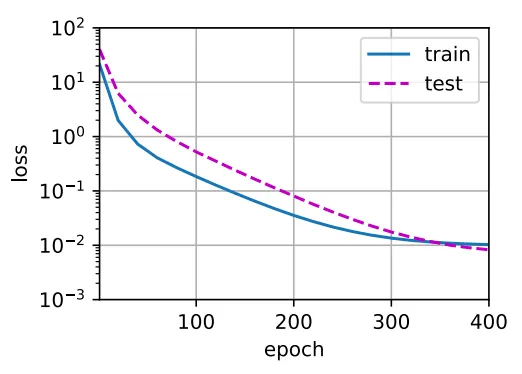
(1) 3차 다항식 함수로 정의하고 학습(weight 개수가 4개)

training loss가 효과적으로 줄어들고 있음을 확인할 수 있습니다.

2)1차 다항식 함수로 정의하고 학습(weight 개수가 2개)

3차 함수로 표현되는 데이터를 1차 함수로 표현하려다 보니 당연하게도 데이터를 제대로 묘사하지 못하고 오차가 많이 발생하게 됩니다. 이에 대한 결과로 training loss가 일정 값 아래로 내려가지 않고 있습니다. 위와 같은 non-linear pattern을 linear model로 적합시키려 하면 Underfitting이 발생하게 됩니다.

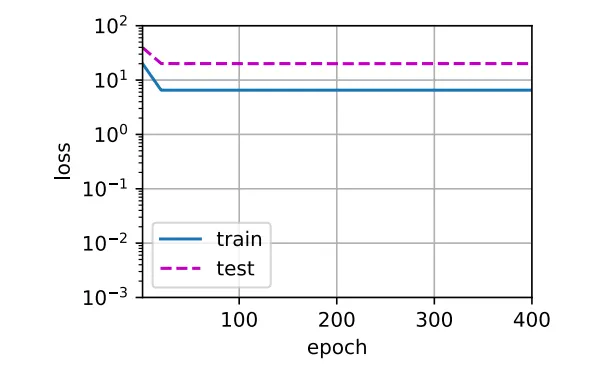
3)고차(>>3) 다항식으로 정의하고 학습 (weight 개수가 너무 많다)

이러한 상황에서는 고차 계수(4차 이상)의 값이 0에 가까워야 한다는 것을 학습하기 위한 데이터가 부족한 상태이고 이런 상황에서 지나치게 복잡한 모델은 Training dataset의 noise에 영향을 많이 받게 됩니다. Training Loss는 효과적으로 줄일 수 있지만, Test Loss은 높은 값을 유지하게 되어버려 결국 Overfitting이 발생하게 됩니다.

그렇다면 이러한 Overfitting, Underfitting issue를 해결하기 위한 방법은 어떤 것이 있을까요?

4.5 Weight Decay

앞서 제시한 Overfitting을 제어하기 위해, training datasets을 늘리는 것이 좋다고 하였습니다. 하지만 데이터를 추가적으로 얻는것은 현실적으로 쉽지 않은 일입니다. 또한 차수를 조절하여 함수의 Complexity를 조절하는 것도 한계가 있습니다.

그래서 우리는 함수의 Complexity를 조금 더 우아하게 조정하는 tool을 사용할 것입니다.

4.5.1 Norms and Weight Decay

그 중 하나가 바로 weight decay입니다. regularization technique중 하나 인데요. 예를 들어, linear function

f(\mathbf{x})=\mathbf{w}^{\top} \mathbf{x}

를 가정 하였을 때, 이 함수의 Complexity는

\|\mathbf{w}\|^{2}

로 표현 됩니다. 이 값이 작을 수록 함수가 더 단순해 지는 것입니다. (

l_2

norm 사용) 이 값을 계속 작게 유지하기 위해 이 값을 penalty로 취급하고 loss에 추가를 합니다. training label에 대한 예측 오차 줄이기 에서 예측 오차 + penalty norm 두개 다 줄이기로 목표가 변경이 되었습니다. 이렇게 되면 만약 weight이 너무 커지면 Training Error를 줄이는 것보다 weight를 줄이는 것을 우선적으로 하게 만들기 때문에 complexity를 조절할 수 있습니다. 식으로 표현하면 아래와 같습니다.

l(\mathbf{w}, b)=\frac{1}{n} \sum_{i=1}^{n} \frac{1}{2}\left(\mathbf{w}^{\top} \mathbf{x}^{(i)}+b-y^{(i)}\right)^{2} \\l(\mathbf{w}, b)+\frac{\lambda}{2}\|\boldsymbol{w}\|^{2}

이러한 regularization을 조절하기 위해, 우리는

\lambda

를 추가하여 조절합니다. 이 값은 hyperparameter로써 사용자가 조절해야 하는 값입니다. 이렇게 다시 Loss function을 정의한 후 Training을 통해

\mathbf{w}

를 업데이트 해 나갑니다.

\mathbf{w} \leftarrow(1-\eta \lambda) \mathbf{w}-\frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{R}} \mathbf{x}^{(i)}\left(\mathbf{w}^{\top} \mathbf{x}^{(i)}+b-y^{(i)}\right)

이러한 방법을 통해 weight을 줄여가며 complexity를 줄여 나갑니다. 파라미터의 개수를 직접 조절해가며 complexity를 조절하는 것보단 훨씬 나은 방법인 거 같습니다!

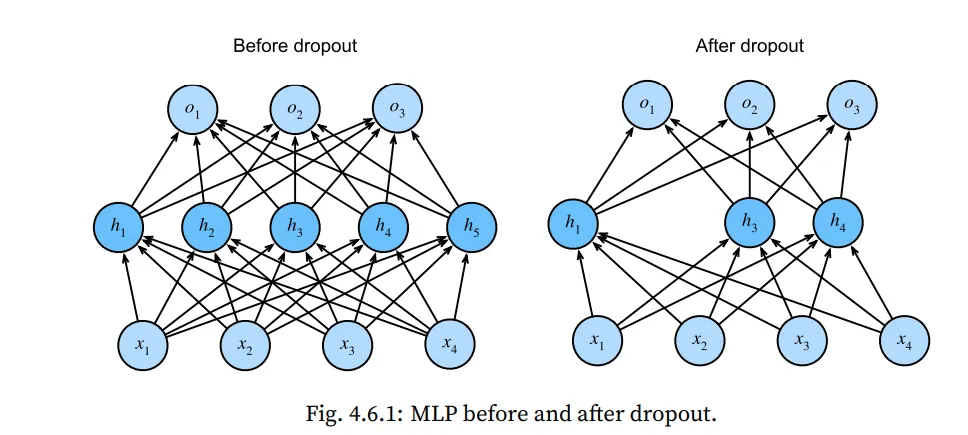
4.6 Dropout

Dropout은 전체 모든 weight를 training에 참여시키지 않고, 일부만 참여시키는 방법입니다. 속담에 “사공이 많으면 배가 산으로 간다” 라는 말이 있듯, 이 방법은 사공을 몇 명 줄이는 방식으로 진행됩니다. 이 때 이 사공들을 확률

p

를 따라 무작위로 뽑는 것입니다. 학습을 할 때마다 매번 무작위로 hidden unit을 제거해 training을 진행시키는 방식입니다.

4.6.3 Dropout in Practice .

Dropout을 hidden layer에 사용한다는 것은 각 hidden unit에 확률

p

를 가지고 0으로 만듭니다. (제거) 아래 그림을 살펴보면,

h_2

와

h_5

가 제거된 것을 알수 있습니다. 결과적으로 출력을 계산할 때, 출력은 더이상

h_{1}, \ldots, h_{5}

중 어느 하나에도 의존하지 않게 됩니다. 이렇게 함으로써 어떤 특정 feature에 매몰되는 현상을 줄여 overfitting을 줄입니다.

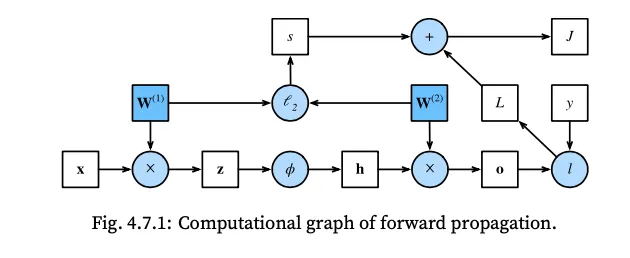
4.7 Forward Propagation, Backward Propagation, and Computational Graphs

아래 모델의 특징

•

한 개의 hidden layer를 가집니다.

•

l2l_2l2​ norm regularization을 적용하였습니다.

4.7.1 Forward Propagation

\mathbf{z}=\mathbf{W}^{(1)} \mathbf{x}\\ \mathbf{h}=\phi(\mathbf{z})\\\mathbf{o}=\mathbf{W}^{(2)} \mathbf{h}\\L=l(\mathbf{o}, y)\\s=\frac{\lambda}{2}\left(\left\|\mathbf{W}^{(1)}\right\|_{F}^{2}+\left\|\mathbf{W}^{(2)}\right\|_{F}^{2}\right)\\J=L+s

4.7.2 Computational Graph of Forward Propagation

4.7.3 Backpropagation

\frac{\partial J}{\partial L}=1 \text { and } \frac{\partial J}{\partial s}=1 \\ \frac{\partial J}{\partial \mathbf{o}}=\operatorname{prod}\left(\frac{\partial J}{\partial L}, \frac{\partial L}{\partial \mathbf{o}}\right)=\frac{\partial L}{\partial \mathbf{o}} \in \mathbb{R}^{q} \\ \frac{\partial s}{\partial \mathbf{W}^{(1)}}=\lambda \mathbf{W}^{(1)} \text { and } \frac{\partial s}{\partial \mathbf{W}^{(2)}}=\lambda \mathbf{W}^{(2)} \\ \frac{\partial J}{\partial \mathbf{W}^{(2)}}=\operatorname{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{W}^{(2)}}\right)+\operatorname{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(2)}}\right)=\frac{\partial J}{\partial \mathbf{o}} \mathbf{h}^{\top}+\lambda \mathbf{W}^{(2)} \\ \frac{\partial J}{\partial \mathbf{h}}=\operatorname{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{h}}\right)=\mathbf{{W}^{(2)}}^{\top} \frac{ \partial J}{\partial \mathbf{o}} \\ \frac{\partial J}{\partial \mathbf{z}}=\operatorname{prod}\left(\frac{\partial J}{\partial \mathbf{h}}, \frac{\partial \mathbf{h}}{\partial \mathbf{z}}\right)=\frac{\partial J}{\partial \mathbf{h}} \odot \phi^{\prime}(\mathbf{z}) \\ \frac{\partial J}{\partial \mathbf{W}^{(1)}}=\operatorname{prod}\left(\frac{\partial J}{\partial \mathbf{z}}, \frac{\partial \mathbf{z}}{\partial \mathbf{W}^{(1)}}\right)+\operatorname{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(1)}}\right)=\frac{\partial J}{\partial \mathbf{z}} \mathbf{x}^{\top}+\lambda \mathbf{W}^{(1)}

4.7.4 Training Neural Networks

Neural Network를 training 하는 경우, Forward Propagation 과정에서 우리는 식의 방향대로 연산을 수행하고 그 과정에서 계산되는 모든 변수의 값을 저장한다. 그리고 그 값들이 Backpropagation 과정에서 다시 사용됩니다.

이러한 이유 때문에 Backpropagation과정에서 메모리를 많이 사용하게 됩니다.

4.8 Numerical Stability and Initialization

Activation function을 잘 선택해야 알고리즘을 Loss를 빠르게 줄여나갈수 있고 또한 특별히 정의하지 않았던 초기 파라미터 값들을 어떻게 설정해야할지를 공부해야합니다.

4.8.1 Vanishing and Exploding Gradients

입력이

x

, 출력이

o

이고

L

layers를 가지는 네트워크를 가정해보겠습니다.

\mathbf{h}^{(l)}=f_{l}\left(\mathbf{h}^{(l-1)}\right) \text { and thus } \mathbf{o}=f_{L} \circ \ldots \circ f_{1}(\mathbf{x}) \\\partial_{\mathbf{W}^{(l)}} \mathbf{o}=\partial_{\mathbf{h}^{(L-1)}} \mathbf{h}^{(L)} \cdot \ldots \cdot \partial_{\mathbf{h}^{(l)}} \mathbf{h}^{(l+1)} \partial_{\mathbf{W}^{(l)}} \mathbf{h}^{(l)}

앞서 제시한 backpropagation 과정에서의 chain rule 때문에 임의의 layer의 weight의 편미분값을 구하기 위해선 많은 행렬의 곱의 형태로 표현됩니다. 따라서 값이 엄청나게 커지거나 작아지거나 할 가능성이 있습니다. 이렇게 되면 Loss 값을 수렴시키기 어려워집니다.

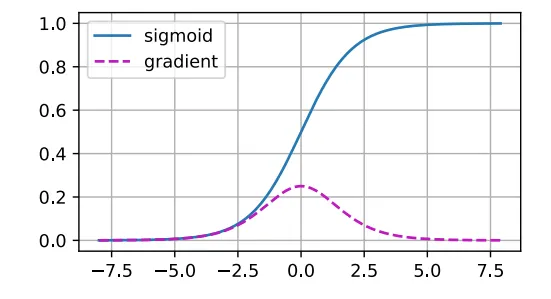
앞서 제시한 Sigmoid function이 그 중 한가지 사례입니다.

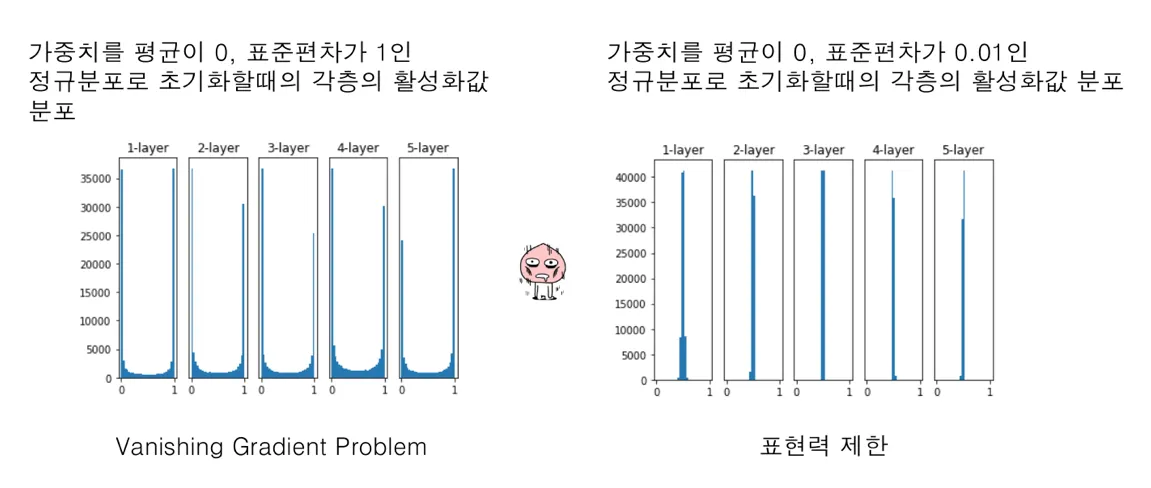
sigmoid의 gradient값이 대략 [-4,4]범위에 들어가지 않는 수이면 값은 거의 0으로 수렴하는 것을 확인할수 있습니다. 따라서 곱의 형태로 표현되는 gradient 값이 0에 가까워져 소멸하게 되여 학습을 제대로 진행하지 못하게 됩니다. 따라서 우린 sigmoid 보다는 ReLU를 주로 사용합니다.

4.8.2 Parameter Initialization

”어디서 출발해야 산을 잘 내려갈 수 있을까?”

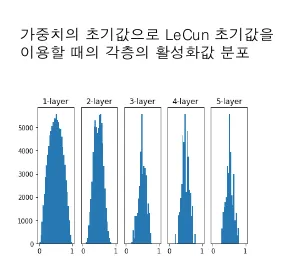
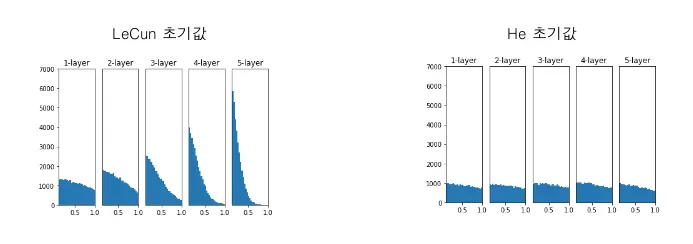
앞서 다룬 Vanishing/Exploding Gradients 문제를 해결하기 위한 방법이 바로 Weight Initialization이다. 위에서 언급한듯이 딥러닝은 BackPropagation 과정이 가장 중요한 과정이다. 가중치 초기화를 0으로 하면 초기 gradient 값이 소멸되고 너무 크거나 작은 값으로 하게되면 학습이 잘 되지 않는다. 이런 가중치 초기화를 하는데 있어서 가장 많이 사용하는 2가지 방법이 있다.

(1) Xavier initialization → Sigmoid, Tanh

(2) He initialization → ReLU

\begin{aligned} &\text LeCun\,Initialization :\quad W \sim N\left(0, \frac{1}{n_{i n}}\right) \\ &\text Xavier\,Initialization :\quad W \sim N\left(0, \frac{2}{n_{i n}+n_{\text {out }}}\right) \end{aligned}

\text { He initialization: } W \sim N\left(0, \frac{2}{n_{i n}}\right)

4.9 Environment and Distribution Shift

Training dataset에서 잘 훈련하고 test dataset에서 잘 동작하지 않는다 → Overfitting이 아닐까? 가 지금까지의 결론.

Understanding Dataset Shift (미완성)

그러나 test dataset과 training dataset의 분포가 아예 다르기 때문에 잘 동작하지 않는 것일 수 있다.

4.9.1 Types of Distribution Shift

Covariate Shift
입력의 분포는 시간에 따라 달라지는데, 조건부 분포인 P(y∣x)P(y \mid \mathbf{x})P(y∣x) 가 바뀌지 않는 것.

Label Shift
위의 경우와 반대 - 출력의 분포가 달라지고, 조건부 분포 P(x∣y)P(\mathbf{x} \mid y)P(x∣y) 가 바뀌지 않는 것

Concept Shift
label의 정의 자체가 달라지는 것 

4.9.2 Examples of Distribution Shift

자율 주행차를 만들기 위해 머신러닝 알고리즘을 이용할 경우, 가장 중요한 것은 도로 탐지입니다. 실제 데이터를 얻기엔 너무 비싸서 렌더링 엔진 상에서 얻은 데이터를 이용하는 경우 가상 환경에서는 잘 동작했을 알고리즘이라도, 실제 환경에서는 제대로 동작 하지 않을 수 있습니다. 왜냐하면 도로가 너무 단순한 텍스쳐로 되어 있어 도로의 “특징”을 너무 빨리 익혀버리기 때문입니다.