Linear Algebra
///
///
💶

3D Coordinates and Representations of Rotations

생성일
2022/01/28 04:39
태그
Euler Angle
Axis-angle
Quaternion

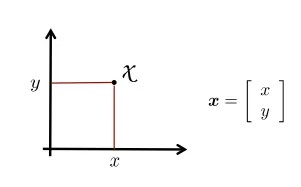
모든 기하학적인 문제의 출발은 2D 또는 3D 상의 한 점을 표현 하는 것입니다.

2D 상의 한 점
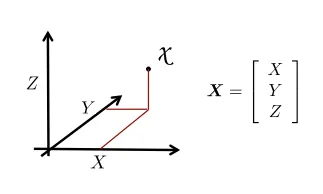
3D 상의 한 점

Representations of Rotation

Rotation을 표현 하는 방법에는 크게 4가지가 존재한다!

[첫번째] Rotation Matrix

3 by 3 matrix를 설정하여 벡터에 이 행렬을 곱하면 임의의 각도만큼 회전한 벡터가 나오는 행렬
R=[r11r12r13r21r22r23r31r32r33]=[c1,c2,c3]=[r1⊤r2⊤r3⊤]R=\left[\begin{array}{lll}r_{11} & r_{12} & r_{13} \\r_{21} & r_{22} & r_{23} \\r_{31} & r_{32} & r_{33}\end{array}\right]=\left[\boldsymbol{c}_{1}, \boldsymbol{c}_{2}, \boldsymbol{c}_{3}\right]=\left[\begin{array}{c}\boldsymbol{r}_{1}^{\top} \\\boldsymbol{r}_{2}^{\top} \\\boldsymbol{r}_{3}^{\top}\end{array}\right]
rotation matrix는 아래 constraints을 만족한다.
∣c1∣2=1, ∣c2∣2=1, ∣c3∣2=1, c1⊤c2=0, c2⊤c3=0, c3⊤c1=0\begin{array}{cccc} & \left|c_{1}\right|^{2}=1 ,\, \left|c_{2}\right|^{2}=1 ,\, \left|c_{3}\right|^{2}=1 ,\,c_{1}^{\top} c_{2}=0 ,\, c_{2}^{\top} c_{3}=0 ,\, c_{3}^{\top} c_{1}=0\end{array}
•
일반적인 3 by 3 matrix의 경우 9 degree of freedom을 가지겠지만, 앞서 제시한 6개의 독립적인 constraints 때문에 3 dof를 가진다.
•
column vector cic_i 는 unit vector eie_i 를 rotation matrix를 통해 mapping 시킨 것과 같다.
•
rotation matrix RR 은 ∣R∣=1,R−1=R⊤|R|=1, R^{-1}=R^{\top} 을 만족한다.
•
상태 추정을 하는데 직접 사용하기에 부적합하며(9개 파라미터 + constraints : 계산량이 넘 많아요) 주로 다른 형식으로 변환하여 회전 과정 진행

[두번째] Euler Angle

•
회전을 시각화할때 유용하다 (비행기, 자동차, 로봇 등등 실제 오브젝트에서 회전 표현 용이)
•
최소 3개의 파라미터가 필요하다 → 3 dof
•
가장 자주 쓰이는 방향 순서는 Z → Y → X
•
gimbal lock 현상이 존재한다 + Discontinuity
•
일반적인 state estimation 할 때 차선책 정도로 쓰인다.
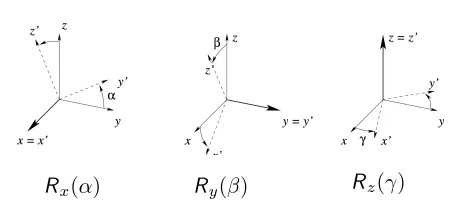
3개의 고정된 축을 기준으로 회전을 순차적으로 진행하면서 회전을 표현한다. (ex. z - y - x axes) 이 때 회전축은 그 전에 회전한 축을 기준으로 돌아간다. (회전축이 고정되지 않음) 각각의 축을 이용한 회전을 식으로 표현하면 다음과 같다.
Rx(φ)=[1000cos⁡φ−sin⁡φ0sin⁡φcos⁡φ]Ry(φ)=[cos⁡φ0sin⁡φ010−sin⁡φ0cos⁡φ]Rz(φ)=[cos⁡φ−sin⁡φ0sin⁡φcos⁡φ0001]\begin{array}{l}R_{x}(\varphi)=\left[\begin{array}{ccc}1 & 0 & 0 \\0 & \cos \varphi & -\sin \varphi \\0 & \sin \varphi & \cos \varphi\end{array}\right] \\R_{y}(\varphi)=\left[\begin{array}{ccc}\cos \varphi & 0 & \sin \varphi \\0 & 1 & 0 \\-\sin \varphi & 0 & \cos \varphi\end{array}\right] \\R_{z}(\varphi)=\left[\begin{array}{ccc}\cos \varphi & -\sin \varphi & 0 \\\sin \varphi & \cos \varphi & 0 \\0 & 0 & 1\end{array}\right]\end{array}
Euler angle representation의 가장 큰 특징은 회전을 진행할 때 어떤 축을 먼저 회전하는지에 따라 회전이 달라진다는 것이다. 아래의 회전의 식을 보면 알수 있겠지만 같은 축, 같은 각도로 회전을 시켜도 무슨 축을 먼저 돌렸는지에 따라 rotation matrix가 달라짐을 확인할 수 있다.

회전 1 (1 → 2 → 3)

RA(α,β,γ)=R3(γ)R2(β)R1(α)[cos⁡γcos⁡β−sin⁡γcos⁡α+cos⁡γsin⁡βsin⁡αsin⁡γsin⁡α+cos⁡γsin⁡βcos⁡αsin⁡γcos⁡βcos⁡γcos⁡α+sin⁡γsin⁡βsin⁡α−cos⁡γsin⁡α+sin⁡γsin⁡βcos⁡α−sin⁡βcos⁡βsin⁡αcos⁡βcos⁡α]\begin{array}{l}R_{A}(\alpha, \beta, \gamma)=R_{3}(\gamma) R_{2}(\beta) R_{1}(\alpha) \\{\left[\begin{array}{ccc}\cos \gamma \cos \beta & -\sin \gamma \cos \alpha+\cos \gamma \sin \beta \sin \alpha & \sin \gamma \sin \alpha+\cos \gamma \sin \beta \cos \alpha \\\sin \gamma \cos \beta & \cos \gamma \cos \alpha+\sin \gamma \sin \beta \sin \alpha & -\cos \gamma \sin \alpha+\sin \gamma \sin \beta \cos \alpha \\-\sin \beta & \cos \beta \sin \alpha & \cos \beta \cos \alpha\end{array}\right]}\end{array}

회전 2 (3 → 2 → 1)

RB(α,β,γ)=R1(α)R2(β)R3(γ)[cos⁡γcos⁡β−sin⁡γcos⁡βsin⁡βcos⁡γsin⁡βsin⁡α+sin⁡γcos⁡α−sin⁡γsin⁡βsin⁡α+cos⁡γcos⁡α−cos⁡βsin⁡α−cos⁡γsin⁡βcos⁡α+sin⁡γsin⁡αsin⁡γsin⁡βcos⁡α+cos⁡γsin⁡αcos⁡βcos⁡α]\begin{array}{l}R_{B}(\alpha, \beta, \gamma)=R_{1}(\alpha) R_{2}(\beta) R_{3}(\gamma) \\{\left[\begin{array}{ccc}\cos \gamma \cos \beta & -\sin \gamma \cos \beta & \sin \beta \\\cos \gamma \sin \beta \sin \alpha+\sin \gamma \cos \alpha & -\sin \gamma \sin \beta \sin \alpha+\cos \gamma \cos \alpha & -\cos \beta \sin \alpha \\-\cos \gamma \sin \beta \cos \alpha+\sin \gamma \sin \alpha & \sin \gamma \sin \beta \cos \alpha+\cos \gamma \sin \alpha & \cos \beta \cos \alpha\end{array}\right]}\end{array}

[3번째] Axis - Angle Representation

•
rotation axis를 표현하는 벡터와 rotation angle을 표현하는 스칼라의 형태로 회전을 표현
•
총 4개의 파라미터 사용! (3 for axis vector + 1 for angle scalar)
•
Singularity가 θ=0\theta = 0 에서 존재합니다.
•
회전이 (−π,π](-\pi, \pi] 구간으로 제한됩니다.
•
연속되는 회전을 표현할 수 없습니다. (rotation matrix 로 변형해서 구해야 합니다.)
•
인간이 보기 편한 형태입니다.
총 4개의 파라미터로 표현하며, normalize할 경우 3개의 파라미터로 표현할 수도 있다. (Minimal)
θ,r=[r1,r2,r3]⊤ with ∥r∥=1\theta, \boldsymbol{r}=\left[r_{1}, r_{2}, r_{3}\right]^{\top} \quad \text { with } \quad\|\boldsymbol{r}\|=1
r=[r1,r2,r3]⊤ with ∥r∥=θ\boldsymbol{r}=\left[r_{1}, r_{2}, r_{3}\right]^{\top} \quad \text { with } \quad\|\boldsymbol{r}\|=\theta

[4번째] Quaternion

•
3차원 Complex component로 구성된 Complex number로 구성되어 구한다
•
4개의 파라미터가 필요하며, 회전을 표현하는 것이 unique합니다.
•
Singularity 와 discontinuities 가 없습니다.
Quaternion을 수학적으로 정의하면 4D-Vector의 형태를 가진다.
q=[qq] with q=[q1,q2,q3]⊤q=q+q1i+q2j+q3k=(q,q)\mathbf{q}=\left[\begin{array}{l}q \\\boldsymbol{q}\end{array}\right] \quad \text { with } \quad \boldsymbol{q}=\left[q_{1}, q_{2}, q_{3}\right]^{\top} \\ \mathbf{q}=q+q_{1} i+q_{2} j+q_{3} k =(q, \boldsymbol{q})
quaternion은 기본적인 대수법칙들을 만족합니다.
•
Addition : q=(q,q),(p,p)=(q+r,q+r)\mathbf{q}=(q, \boldsymbol{q}), \quad (p, \boldsymbol{p})=(q+r, \boldsymbol{q}+\boldsymbol{r})
•
Multiplication : p=qr,(p,p)=(qr−q⋅r,rq+qr+q×r)\begin{aligned}\mathbf{p} &=\mathbf{q r}, \quad (p, \boldsymbol{p}) =(q r-\boldsymbol{q} \cdot \boldsymbol{r}, r \boldsymbol{q}+q \boldsymbol{r}+\boldsymbol{q} \times \boldsymbol{r})\end{aligned} → not cummutative
•
Inverse : q−1=q∗∣q∣2,withq∗=[q−q],∣q∣2=q02+q12+q22+q32\mathbf{q}^{-1}=\frac{\mathbf{q}^{*}}{|\mathbf{q}|^{2}},\quad \text{with} \quad \mathrm{q}^{*}=\left[\begin{array}{c} q \\ -\boldsymbol{q} \end{array}\right], \quad |\mathbf{q}|^{2}=q_{0}^{2}+q_{1}^{2}+q_{2}^{2}+q_{3}^{2}

Quaternion을 회전으로 표현하기

앞서 axis-angle rotation representation 처럼 축과 각도를 쿼터니언에 표현하면 된다.
q=[qq]=[cos⁡(θ/2)sin⁡(θ/2)r]\mathbf{q}=\left[\begin{array}{l}q \\\boldsymbol{q}\end{array}\right]=\left[\begin{array}{c}\cos (\theta / 2) \\\sin (\theta / 2) \boldsymbol{r}\end{array}\right]
이 때, rr 은 normalized rotation axis로써 아래의 성질을 만족한다.
r=[r1,r2,r3]⊤ with ∥r∥=1\boldsymbol{r}=\left[r_{1}, r_{2}, r_{3}\right]^{\top} \text { with }\|\boldsymbol{r}\|=1

예시) r=[0.60.80.0]r=\left[\begin{array}{l}0.6 \\0.8 \\0.0\end{array}\right]을 축으로 하여 θ=30∘\theta=30^{\circ} 만큼 회전할 때, quaternion으로 표현해!

q=[cos⁡(15∘)sin⁡(15∘)[0.60.80.0]]\mathbf{q}=\left[\begin{array}{c}\cos \left(15^{\circ}\right) \\\sin \left(15^{\circ}\right)\left[\begin{array}{l}0.6 \\0.8 \\0.0\end{array}\right]\end{array}\right]
q=(cos⁡(15∘),sin⁡(15∘)(0.6,0.8,0.0))q=cos⁡(15∘)+sin⁡(15∘)(0.6i+0.8j+0.0k)\begin{array}{l}\mathbf{q}=\left(\cos \left(15^{\circ}\right), \sin \left(15^{\circ}\right)(0.6,0.8,0.0)\right) \\\mathbf{q}=\cos \left(15^{\circ}\right)+\sin \left(15^{\circ}\right)(0.6 i+0.8 j+0.0 k)\end{array}
우리에게 주어진 임의의 벡터를 주어진 각도와 축을 가지고 회전시킬 때 아래의 공식을 이용한다. 이 때, 주어지는 벡터는 p=(0,p)\mathbf{p}=(0, \boldsymbol{p}) 의 형태로 표현하며 벡터 p\boldsymbol{p} 로 주어진 벡터의 3차원을 표현한다. (스칼라 값은 0임을 기억하자), 그리고 회전을 나타내는 쿼터니언을 q\mathbf{q} 라고 정의하면 아래와 같이 연산한다.
p′=qpq−1\mathbf{p}^{\prime}=\mathbf{q p q}^{-1}

Quaternion을 이용해 연속적으로 회전시키기

연속된 rotation은 quaternion multiplication을 통해 쉽게 이루어진다.
p′=q′pq′−1,p′′=q′′p′q′′−1\mathbf{p}^{\prime}=\mathbf{q}^{\prime} \mathbf{p q}^{\prime-1}, \quad \mathbf{p}^{\prime \prime}=\mathbf{q}^{\prime \prime} \mathbf{p}^{\prime} \mathbf{q}^{\prime \prime-1}
p′′=q′′(q′pq′−1)q′′−1=(q′′q′)p(q′−1q′′−1)=(q′′q′)⏟qp(q′′q′)−1⏟q−1=qpq−1\begin{aligned}\mathbf{p}^{\prime \prime} &=\mathbf{q}^{\prime \prime}\left(\mathbf{q}^{\prime} \mathbf{p} \mathbf{q}^{\prime-1}\right) \mathbf{q}^{\prime \prime-1} \\&=\left(\mathbf{q}^{\prime \prime} \mathbf{q}^{\prime}\right) \mathbf{p}\left(\mathbf{q}^{\prime-1} \mathbf{q}^{\prime \prime-1}\right) \\&=\underbrace{\left(\mathbf{q}^{\prime \prime} \mathbf{q}^{\prime}\right)}_{\mathbf{q}} \mathbf{p} \underbrace{\left(\mathbf{q}^{\prime \prime} \mathbf{q}^{\prime}\right)^{-1}}_{\mathbf{q}^{-1}} \\&=\mathbf{q p q}^{-1}\end{aligned}
rotation q\mathbf{q} 는 각각의 회전을 의미하는 q′′,q′\mathbf{q}^{\prime \prime}, \mathbf{q}^{\prime} 의 곱의 형태로 표현 할수 있다. q=q′′q′\mathbf{q}=\mathbf{q}^{\prime \prime} \mathbf{q}^{\prime} 로 나타낸다. rotation matrix 형태로 표현한다면 Rq=Rq′′Rq′R_{\mathbf{q}}=R_{\mathbf{q}^{\prime \prime}} R_{\mathbf{q}^{\prime}} 의 형태로 나타내는 것과 같다.

Rotation 표현방법 비교해보기

•
Rotation matrix는 교환되는 형식으로써 역할을 한다.(이 행렬을 통해 다른 표현들로 바꿔 표현)
•
state estimation은 주로 quaternion을 통해 이루어진다.
•
angle-axis 표현 방법은 사람이 읽기에 좋다. (quaternion과 연계되어 사용)
이러한 특징들을 표로 나타내면 아래와 같다.
위의 제시한 4가지 방법은 서로서로 변환하는 공식이 이미 존재하고 이에 해당하는 계산기 또한 나와있다.
3D Rotation Converter
https://www.andre-gaschler.com/rotationconverter/
Made with