Linear Algebra
///
///
👞

2. Least Squares Problem

태그
Least Squares
Gram-Schmidt
QR-decomposition

Inner Product

벡터 u,v∈Rn\mathbf{u}, \mathbf{v} \in \mathbb{R}^{n} 가 주어졌을 때 각 벡터는 n×1n \times 1 행렬로 생각할 수 있고, uT\mathbf{u}^{T} 는 1×n1 \times n 행렬로 생각할 수 있다. uTv\mathbf{u}^{T}\mathbf{v} 를 inner product 혹은 dot product 로 정의하며 u⋅v\mathbf{u} \cdot \mathbf{v} 로 표기한다.
inner product는 아래와 같은 성질을 만족한다. (u,v\mathbf{u}, \mathbf{v}는 벡터, cc 는 스칼라)
u⋅v=v⋅u(u+v)⋅w=u⋅w+v⋅w(cu)⋅v=c(u⋅v)=u⋅(cv)u⋅u≥0, and u⋅u=0 if and only if u=0\begin{array}{l}\mathbf{u} \cdot \mathbf{v}=\mathbf{v} \cdot \mathbf{u} \\(\mathbf{u}+\mathbf{v}) \cdot \mathbf{w}=\mathbf{u} \cdot \mathbf{w}+\mathbf{v} \cdot \mathbf{w} \\(c \mathbf{u}) \cdot \mathbf{v}=c(\mathbf{u} \cdot \mathbf{v})=\mathbf{u} \cdot(c \mathbf{v}) \\\mathbf{u} \cdot \mathbf{u} \geq \mathbf{0}, \text { and } \mathbf{u} \cdot \mathbf{u}=\mathbf{0} \text { if and only if } \mathbf{u}=\mathbf{0}\end{array}
또한 inner product는 각 벡터의 norm과 angle을 이용해 표현할 수도 있다.
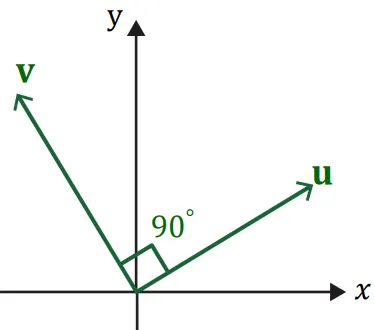
u⋅v=∥u∥∥v∥cos⁡θ\mathbf{u} \cdot \mathbf{v}=\|\mathbf{u}\|\|\mathbf{v}\| \cos \theta
이 때, 만약 u⋅v=0\mathbf{u} \cdot \mathbf{v}=0 을 만족한다면 서로 orthogonal 하다고 한다.
θ=90°\theta = 90\degree를 만족하기 때문에 내적값이 0이 된 것이며 벡터 u,v\mathbf{u}, \mathbf{v} 는 서로 수직이다.

Vector Norm

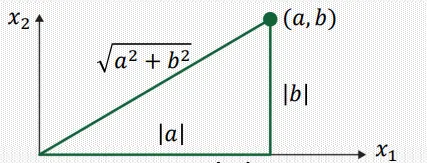
v∈Rn\mathbf{v} \in \mathbb{R}^{n}에 대하여, length (혹은 norm)은 v⋅v\mathbf{v} \cdot \mathbf{v} 의 제곱근으로 정의되며, 양수의 스칼라값으로 정의된다.
∥v∥=v⋅v=v12+v22+⋯+vn2 and ∥v∥2=v⋅v\|\mathbf{v}\|=\sqrt{\mathbf{v} \cdot \mathbf{v}}=\sqrt{v_{1}^{2}+v_{2}^{2}+\cdots+v_{n}^{2}} \text { and }\|\mathbf{v}\|^{2}=\mathbf{v} \cdot \mathbf{v}
이러한 norm은 기하학적으로 원점으로부터 v\mathbf{v} 까지를 잇는 선의 길이를 의미한다.
또한 임의의 scalar 값 cc에 대해, cvc\mathbf{v}의 length는 v\mathbf{v} 의 길이에 ∣c∣|c| 만큼 곱한 값이다.
∥cv∥=∣c∣∥v∥\|c \mathbf{v}\|=|c|\|\mathbf{v}\|
참고로, length가 1인 벡터를 unit vector 라고 한다.
vector를 normalize 한다는 뜻은, 벡터 v\mathbf{v} 가 주어졌을 때, 그것의 length로 나누어주는 것을말한다.
u=1∥v∥v\mathbf{u}=\frac{1}{\|\mathbf{v}\|} \mathbf{v}
u\mathbf{u} 는 v\mathbf{v} 와 같은 방향을 가리키며, 길이만 다르게 된다. (v\mathbf{v}의 length는 1)

Distance between Vectors in Rn\mathbb{R}^{n}

벡터 u,v∈Rn\mathbf{u}, \mathbf{v} \in \mathbb{R}^{n} 에 대해 distance between u  and  v\mathbf{u}\,\,\text{and}\,\, \mathbf{v} 는 아래와 같이 정의됩니다.
dist⁡(u,v)=∥u−v∥\operatorname{dist}(\mathbf{u}, \mathbf{v})=\|\mathbf{u}-\mathbf{v}\|

Least Squares 문제

변수의 개수(nn) 보다 방정식의 개수(mm)가 더 많은 경우, Over-determined Linear System이다. 일반적으로 이러한 경우는 해가 없다. 하지만 우리는 근사적이라도 값을 구하고 싶다!
Overdetermined system Ax≃bA \mathbf{x} \simeq \mathbf{b} 에 대하여, (A∈Rm×n,b∈Rm, and m≫nA \in \mathbb{R}^{m \times n}, \mathbf{b} \in \mathbb{R}^{m}, \text { and } m \gg n) 이러한 시스템의 해 x^\hat{\mathbf{x}}는 아래 와 같이 정의 된다.
x^=arg⁡min⁡x∥b−Ax∥\hat{\mathbf{x}}=\arg \min _{\mathbf{x}}\|\mathbf{b}-A \mathbf{x}\|
어떤 x\mathbf{x} 를 선택하더라도, 벡터 AxA \mathbf{x}는 Col A\text {Col } A 의 영역 안에 존재하게 될 것이다. 따라서, 우린 벡터 b\mathbf{b} 와 가장 가깝게 위치하는 Col A\text {Col } A 위의 한 점을 찾는것, 그 때의 x^\hat{\mathbf{x}} 를 찾는것이 목표이다.
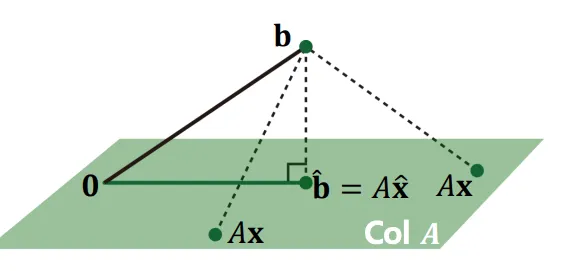
위의 설명을 그림으로 표현하면 아래와 같다.
이 때, 점 b^\hat{\mathbf{b}}은 Col A\text {Col } A 에 존재하는 점 중 점 b\mathbf{b} 와 가장 가까운 점이다. 이러한 조건 하에서 벡터 b−Ax^\mathbf{b}-A \widehat{\mathbf{x}} 는 Col A\text {Col } A 와 반드시 orthogonal 하게 된다. 여기서 벡터 an\mathbf{a}_n은 Col A\text {Col } A 를 구성하는 basis 벡터를 말한다.
(b−Ax^)⊥(x1a1+x2a2⋯+xpan) for any vector x(\mathbf{b}-A \hat{\mathbf{x}}) \perp\left(x_{1} \mathbf{a}_{1}+x_{2} \mathbf{a}_{2} \cdots+x_{p} \mathbf{a}_{n}\right) \text { for any vector } \mathbf{x}
이와 동일하게 서술하면,
(b−Ax^)⊥a1(b−Ax^)⊥a2⋮(b−Ax^)⊥am\begin{array}{c}(\mathbf{b}-A \widehat{\mathbf{x}}) \perp \mathbf{a}_{1} \\(\mathbf{b}-A \hat{\mathbf{x}}) \perp \mathbf{a}_{2} \\\vdots \\(\mathbf{b}-A \widehat{\mathbf{x}}) \perp \mathbf{a}_{m}\end{array}
a1⊤(b−Ax^)=0a2⊤(b−Ax^)=0⋮am⊤(b−Ax^)=0\begin{array}{c}\mathbf{a}_{1}^{\top}(\mathbf{b}-A \hat{\mathbf{x}})=0 \\\mathbf{a}_{2}^{\top}(\mathbf{b}-A \hat{\mathbf{x}})=0 \\\vdots \\\mathbf{a}_{m}^{\top}(\mathbf{b}-A \hat{\mathbf{x}})=0\end{array}
따라서 least squres problem을 푸는 식이 완성된다.
A⊤(b−Ax^)=0A^{\top}(\mathbf{b}-A \hat{\mathbf{x}})=0

Normal Equation

앞서 제시한 Least Squares Problem을 푸는 방법 중 하나가 바로 normal equation입니다. 주어진 least square problem Ax≃bA \mathbf{x} \simeq \mathbf{b}의 식을 풀기 위해 정답에 가장 가까운 해를 구할 것 입니다.
A⊤Ax^=A⊤bA^{\top} A \hat{\mathbf{x}}=A^{\top} \mathbf{b}
해를 구하기 위해 사용하는 식이 위에 제시한 normal equation 입니다.
이러한 형태는 새로운 Linear System Cx=dC \mathbf{x}=\mathbf{d} 의 꼴로 표현할 수 있습니다.
C=A⊤A∈Rn×nd=A⊤b∈RnC=A^{\top} A \in \mathbb{R}^{n \times n} \quad\quad \mathbf{d}=A^{\top} \mathbf{b} \in \mathbb{R}^{n}
만약 C=ATAC=A^{T} A 가 invertible 하다면, 그 해는 아래와 같이 구해질 수 있다.
x^=(A⊤A)−1A⊤b\widehat{\mathbf{x}}=\left(A^{\top} A\right)^{-1} A^{\top} \mathbf{b}
따라서 앞서 주어진 그림을 살펴보았을 때, 점 b\mathbf{b}에서 Col⁡A\operatorname{Col} A로의 orthogonal projection 과정을 아래와 같이 나타낼 수 있다.
b^=f(b)=Ax^=A(A⊤A)−1A⊤b\hat{\mathbf{b}}=f(\mathbf{b})=A \hat{\mathbf{x}}=A\left(A^{\top} A\right)^{-1} A^{\top} \mathbf{b}

만약 C=A⊤AC=A^{\top} A 가 invertible 하지 않다면?

•
CC 가 invertible 하지 않기 위해서는 행렬 AA 가 Linearly dependent 해야한다. (즉, lineary dependent하면 invertible 하다)
•
이러한 경우 해는 항상 무수히 많은 경우가 된다! (→ 해가 없는 경우는 사실상 존재하지 않는다)
•
일반적으로, 현실 데이터셋을 다룰 때 invertible 하지 않은 경우는 없다! (거의 95% 이상) 데이터셋이 많아지면 많아질 수록 feature 간에 linearly dependent한 경우가 높은 확률로 사라지기 때문이다.

Orthogonal and Orthonormal Sets

벡터의 집합 {u1,…,up} in Rn\left\{\mathbf{u}_{1}, \ldots, \mathbf{u}_{p}\right\} \text { in } \mathbb{R}^{n} 에 대햐여, 각 벡터쌍들이 ui⋅uj=0 whenever i≠j\mathbf{u}_{i} \cdot \mathbf{u}_{j}=0 \text { whenever } i \neq j 를 만족하면 orthogonal set이라고 정의한다.
벡터의 집합 {u1,…,up} in Rn\left\{\mathbf{u}_{1}, \ldots, \mathbf{u}_{p}\right\} \text { in } \mathbb{R}^{n} 에 대하여, orthogonal set이라고 가정했을 때, 각 벡터들이 unit vector이다면, orthonormal set이라고 정의한다.
벡터들이 Orthogonal하다면 linearly independent하다고 볼수 있지만, 벡터들이 linearly independent하다고 해서 Orthogonal 하다고 할수 없다.

Orthogonal Projection y^\hat{\mathbf{y}} of y\mathbf{y}

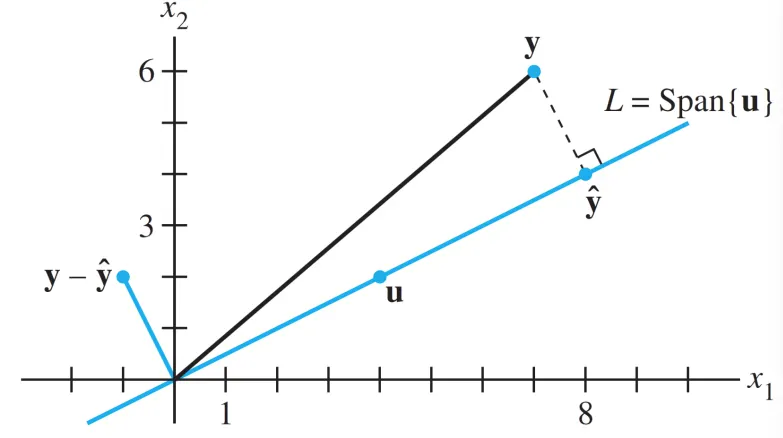
(1) line에 projection하기

one-dimensional subspace L=Span⁡{u}L=\operatorname{Span}\{\mathbf{u}\}에 projection을 한다면 아래와 같은 식으로 표현 가능하다
y^=proj⁡Ly=y⋅uu⋅uu\hat{\mathbf{y}}=\operatorname{proj}_{L} \mathbf{y}=\frac{\mathbf{y} \cdot \mathbf{u}}{\mathbf{u} \cdot \mathbf{u}} \mathbf{u}
만약, 벡터 u\mathbf{u}가 unit vector라면, 아래와 같이 표현할 수도 있다.
y^=proj⁡Ly=(y⋅u)u\hat{\mathbf{y}}=\operatorname{proj}_{L} \mathbf{y}=(\mathbf{y} \cdot \mathbf{u}) \mathbf{u}

(2) Plane에 projection하기

two-dimensional subspace W=Span⁡{u1,u2}W=\operatorname{Span}\{\mathbf{u_1,u_2}\}에 projection 한다면 아래와 같이 표현한다.
y^=proj⁡Ly=y⋅u1u1⋅u1u1+y⋅u2u2⋅u2u2\hat{\mathbf{y}}=\operatorname{proj}_{L} \mathbf{y}=\frac{\mathbf{y} \cdot \mathbf{u}_{1}}{\mathbf{u}_{1} \cdot \mathbf{u}_{1}} \mathbf{u}_{1}+\frac{\mathbf{y} \cdot \mathbf{u}_{2}}{\mathbf{u}_{2} \cdot \mathbf{u}_{2}} \mathbf{u}_{2}
만약, 벡터 u1,u2\mathbf{u_1,u_2}가 unit vector라면, 아래와 같이 표현할 수도 있다.
y^=proj⁡Ly=(y⋅u1)u1+(y⋅u2)u2\hat{\mathbf{y}}=\operatorname{proj}_{L} \mathbf{y}=\left(\mathbf{y} \cdot \mathbf{u}_{1}\right) \mathbf{u}_{1}+\left(\mathbf{y} \cdot \mathbf{u}_{2}\right) \mathbf{u}_{2}

Transformation: Orthogonal Projection

위에 제시한 orthogonal projection 과정을 식으로 표현하면,
b^=f(b)=(b⋅u1)u1+(b⋅u2)u2=(u1Tb)u1+(u2Tb)u2=u1(u1Tb)+u2(u2Tb)=(u1u1T)b+(u2u2T)b=(u1u1T+u2u2T)b[u1u2][u1Tu2T]b=UUTb⇒ linear transformation! \begin{aligned}\hat{\mathbf{b}} &=f(\mathbf{b})=\left(\mathbf{b} \cdot \mathbf{u}_{1}\right) \mathbf{u}_{1}+\left(\mathbf{b} \cdot \mathbf{u}_{2}\right) \mathbf{u}_{2} \\&=\left(\mathbf{u}_{1}^{T} \mathbf{b}\right) \mathbf{u}_{1}+\left(\mathbf{u}_{2}^{T} \mathbf{b}\right) \mathbf{u}_{2} \\&=\mathbf{u}_{1}\left(\mathbf{u}_{1}^{T} \mathbf{b}\right)+\mathbf{u}_{2}\left(\mathbf{u}_{2}^{T} \mathbf{b}\right) \\&=\left(\mathbf{u}_{1} \mathbf{u}_{1}^{T}\right) \mathbf{b}+\left(\mathbf{u}_{2} \mathbf{u}_{2}^{T}\right) \mathbf{b} \\&=\left(\mathbf{u}_{1} \mathbf{u}_{1}^{T}+\mathbf{u}_{2} \mathbf{u}_{2}^{T}\right) \mathbf{b}\end{aligned} \\ \left[\begin{array}{ll} \mathbf{u}_{1} & \mathbf{u}_{2} \end{array}\right]\left[\begin{array}{l} \mathbf{u}_{1}^{T} \\ \mathbf{u}_{2}^{T} \end{array}\right] \mathbf{b}=U U^{T} \mathbf{b} \Rightarrow \text { linear transformation! }

Gram-Schmidt Orthogonalization

이 방법은 Rn \mathbb{R}^{n}상의 subspace에서 orthogonal 하거나 orthonormal한 basis를 만들기 위해 사용되는 단순한 알고리즘입니다.
W=Span⁡{x1,x2}W=\operatorname{Span}\left\{\mathbf{x}_{1}, \mathbf{x}_{2}\right\} 하는 상황을 가정하였을 때, x1=[360],x2=[122]\mathbf{x}_{1}=\left[\begin{array}{l}3 \\6 \\0\end{array}\right] , \mathbf{x}_{2}=\left[\begin{array}{l}1 \\2 \\2\end{array}\right]이다. 이러한 상황에서 subspace WW 에서의 orthogonal basis를 만들기 위해 사용한다. v1=x1\mathbf{v}_{1}=\mathbf{x}_{1} 이라고 가정한 뒤, v2\mathbf{v}_{2}를 x1\mathbf{x}_{1}에 orthogonal한 벡터라고 생각한다면, 아래 식과 같이 표현할 수 있다.
v2=x2−x2⋅x1x1⋅x1x1=[122]−1545[360]=[002]\mathbf{v}_{2}=\mathbf{x}_{2}-\frac{\mathbf{x}_{2} \cdot \mathbf{x}_{1}}{\mathbf{x}_{1} \cdot \mathbf{x}_{1}} \mathbf{x}_{1}=\left[\begin{array}{l}1 \\2 \\2\end{array}\right]-\frac{15}{45}\left[\begin{array}{l}3 \\6 \\0\end{array}\right]=\left[\begin{array}{l}0 \\0 \\2\end{array}\right]
실제로 v1⋅v2\mathbf{v}_{1}\cdot\mathbf{v}_{2} 를 행해보면 값이 0이 나온다는 것을 알 수있다.

QR Factorization

위에서 언급한 Gram-Schmidt 방법을 이용해 orthonormal vector를 구했는데, 이를 이용해 행렬을 분해하는 방법이 QR Factorization (= QR decomposition)이다. 수학적인 정의는 아래와 같다.
행렬 AA 가 m×nm \times n 의 크기를 갖는 행렬로 주어지고, 각 column들이 linearly independent하다고 가정하면, A=QRA = QR 의 형태로 표현할 수 있다. QQ 는 m×nm \times n 크기의 행렬이고, 각 column들은 Col⁡A\operatorname{Col} A 를 구성하는 orthonormal basis이다. RR 은 n×nn \times n 크기의 upper trinangular 형태를 가지는 행렬이며, 역행렬이 존재한다.
분해하는 과정을 짧게 나마 서술해보면.
1.
주어진 행렬의 column vector들을 나눠놓은 후 각각 Gram-Schmidt 방법을 적용시킨다.
2.
orthogonalize 된 벡터들을 normalize 하기 위해 각각의 norm으로 나눠준다 (크기를 1로 만듬= 정규화)
3.
이 벡터들을 순서대로 모으면 행렬 QQ 가 되고, 이 행렬은 orthonormal 하다.
4.
orthonormal 행렬의 성질 QQ⊤=Q⊤Q=IQ Q^{\top}=Q^{\top} Q=I 을 이용해 R=Q−1A=Q⊤AR = Q^{-1} A=Q^{\top} A 를 유도할 수 있습니다. 이를 이용해 행렬 RR 을 구하면 factorization이 끝난다.
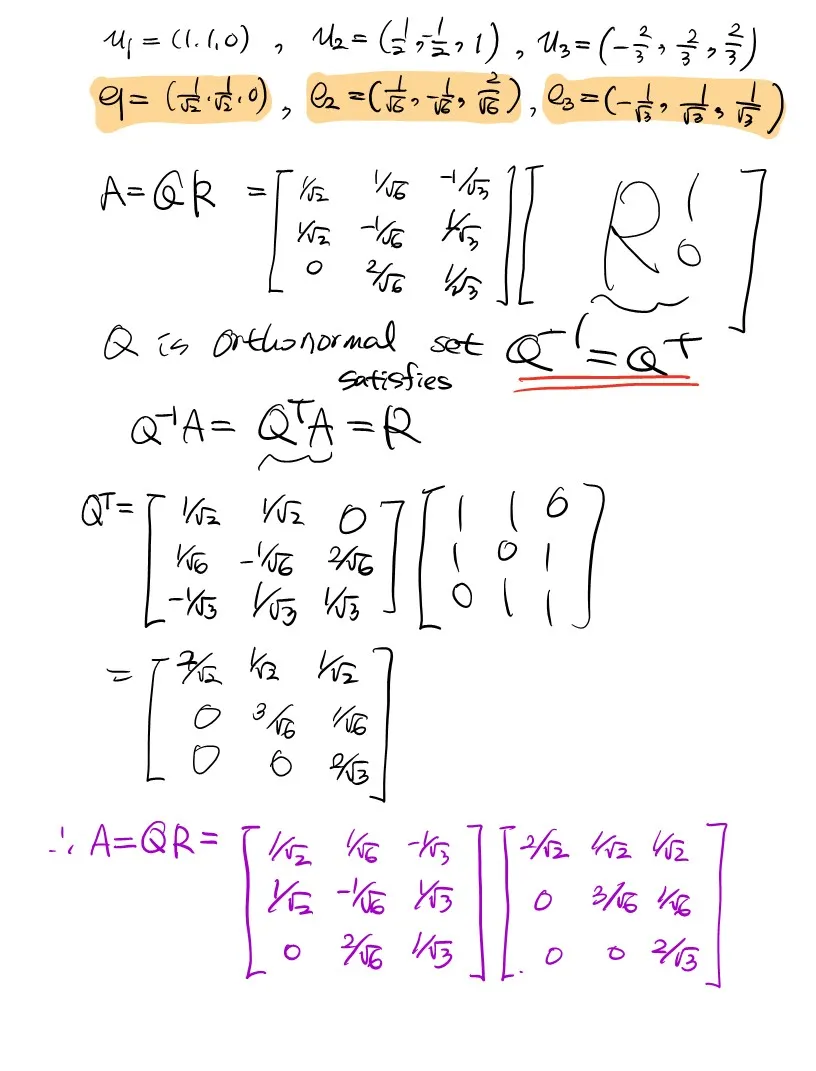
아래 풀이는 임의로 주어진 행렬에 대해 QR decomosition을 해보는 예제이다.

reference

인공지능을 위한 선형대수 오리엔테이션 : edwith
인공지능을 위한 선형대수
https://www.edwith.org/ai251/joinLectures/195088
Made with