Linear Algebra
//
//
✍️

베이즈 필터

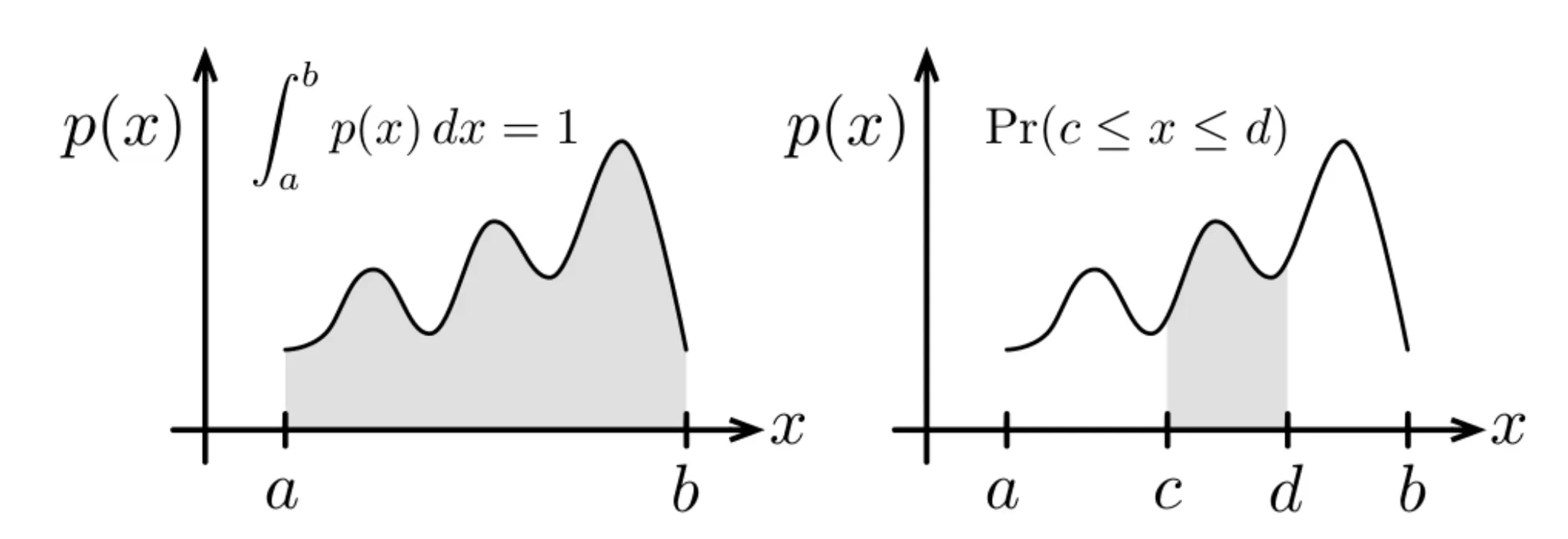
일상 생활에서 우리는 어떠한 현상을 정확히 설명할 수 없기 때문에 확률분포로써 현상을 설명하곤 한다….
또한 우리 주변에 무수히 많은 노이즈가 존재하기 때문에 Randomness에 대해서도 고려할 필요가 있고 이를 위해서라도 확률분포는 너무나도 중요하다!

Marginalization (Law of Total Probability)

여러 사건이 동시에 일어날 확률을 의미하는 Joint Distribution은 아래와 같이 정의한다.
p(x,y)=p(X=x and Y=y)p(x, y)=p(X=x \text { and } Y=y)
이 때, 여러 개의 확률 변수로 이루어진 Joint Distribution에서 한 가지 변수에 대해서만 확률 값을 추정하고 싶다면 어떻게 해야 할까?
간단하다! 나머지 변수에 대해 적분하면 된다! 이 것이 Marginalization이다!
식은 아래와 같이 서술할 수 있다!
p(x)=∑y∈Yp(x,y)=∑y∈Yp(x∣y)p(y)p(x)=\sum_{y \in \mathcal{Y}} p(x, y)=\sum_{y \in \mathcal{Y}} p(x \mid y) p(y)
p(x)=∫y∈Yp(x,y)dy=∫y∈Yp(x∣y)p(y)dyp(x)=\int_{y \in \mathcal{Y}} p(x, y) d y=\int_{y \in \mathcal{Y}} p(x \mid y) p(y) d y

Bayes’ Rule

위 개념을 이용하여 조건부 확률을 구할 때 식을 유도해 볼 수 있다.
일단, 조건부 확률에 대한 기본 식을 살펴보자,
p(x∣y)=p(x,y)p(y)p(x \mid y)=\frac{p(x, y)}{p(y)}
위 식을 적절히 바꾸면 아래와 같이 표현할 수 있다.
p(x,y)=p(x∣y)p(y)=P(y∣x)p(x) p(x, y)=p(x \mid y) p(y)=P(y \mid x) p(x)
위에 제시한 두 식과 앞서 언급한 Marginalization을 이용하면 아래의 식을 만들어낸다.
p(x∣y)=p(y∣x)p(x)p(y)=p(y∣x)p(x)∑x∈Xp(y∣x)p(x)p(x \mid y)=\frac{p(y \mid x) p(x)}{p(y)}=\frac{p(y \mid x) p(x)}{\sum_{x \in \mathcal{X}} p(y \mid x) p(x)}
이를 이해하기 쉽게 표현한다면, 그 유명한 베이즈 법칙이 완성된다. 향후 다룰 모든 내용은 이 베이즈 법칙을 기반으로 작성된 알고리즘들이다.
p( hypothesis ∣ data )=p( data ∣ hypothesis )p( hypothesis )p( data )\begin{aligned}& \\& p(\text { hypothesis } \mid \text { data })=\frac{p(\text { data } \mid \text { hypothesis }) p(\text { hypothesis })}{p(\text { data })} \\& \\&\end{aligned}

추가사항 - 여러개의 변수를 가지는 Bayes’ Rule

Gaussian Distribution

그 중에서도 우리는 가우시안을 주로 사용하곤 하는데… 이는 Central Limit Theorem 때문이다! 동일한 확률분포를 가진 독립 확률 변수 n개의 평균의 분포는 n이 적당히 크다면 정규분포에 가까워진다는 정리인데, 결국 많은 양의 데이터를 다루다 보면 필연적으로 가우시안 분포를 닮게 된다는 말씀!
또한 가우시안을 사용하면 Linear Algebra 형태로 쉽게 풀이할 수 있기 때문에 자주 사용된다.
가우시안을 나타내는 식은 아래와 같다. 흔히들 x∼N(μ,σ2)x \sim \mathcal{N}\left(\mu, \sigma^2\right) 로 나타낸다.
p(x)=12πσ2exp⁡(−12(x−μ)2σ2)p(x)=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left(-\frac{1}{2} \frac{(x-\mu)^2}{\sigma^2}\right)
위는 단항 가우시안이고, 실제로 시스템을 설계한다면,multivariate Gaussian을 사용하는 경우가 많다. 이럴 때 x∼N(μ,Σ)x \sim \mathcal{N}(\mu, \Sigma) 로 나타내곤 하며, 평균과 분산은 각각 μ=E[x]  ,Σ=Cov⁡[x]=E[(x−μ)(x−μ)⊤]\mu=\mathbb{E}[x] \;,\Sigma=\operatorname{Cov}[x]=\mathbb{E}\left[(x-\mu)(x-\mu)^{\top}\right] 를 의미한다.
해당하는 식은 아래와 같다.
p(x)=(2π)−n2∣Σ∣−12exp⁡(−12(x−μ)⊤Σ−1(x−μ))p(x)=(2 \pi)^{-\frac{n}{2}}|\Sigma|^{-\frac{1}{2}} \exp \left(-\frac{1}{2}(x-\mu)^{\top} \Sigma^{-1}(x-\mu)\right)

Gaussian을 Affine Transform하기

이 식은 계~~~~~속 나오게 되는 식이니 꼭 숙지하자. 가우시안이 나오는 한, 칼만 필터가 전개되는 한 꼭 나오더라…!!!
linear Transform은 y=Axy=A x 의 형태를, Affine Transform은 y=Ax+by=A x+b 의 형태를 띄는 변환방법이다.
아래와 같이 두 분포를 정의해보자.
x∼N(μ,Σ) and y=Ax+bx \sim \mathcal{N}(\mu, \Sigma) \text { and } y=A x+b
평균의 성질에 따라 아래와 같이 표현되고,
E[y]=E[Ax+b]=AE[x]+b=Aμ+b\mathbb{E}[y]=\mathbb{E}[A x+b]=A \mathbb{E}[x]+b=A \mu+b
분산의 정의에 따라 아래와 같이 표현된다.
Cov⁡[y]=E[(y−E[y])(y−E[y])⊤]=E[(Ax−Aμ)(Ax−Aμ)⊤]=AE[(x−μ)(x−μ)⊤]A⊤=AΣA⊤\begin{aligned}& \operatorname{Cov}[y]=\mathbb{E}\left[(y-\mathbb{E}[y])(y-\mathbb{E}[y])^{\top}\right] \\& =\mathbb{E}\left[(A x-A \mu)(A x-A \mu)^{\top}\right]=A \mathbb{E}\left[(x-\mu)(x-\mu)^{\top}\right] A^{\top} \\& =A \Sigma A^{\top}\end{aligned}
따라서, 가우시안에 대해 Affine Transform을 진행하게 된다면 그대로 Gaussian이 출력 됨을 알 수 있다. → 이건 정말 매우 really 중요한 성질이다. (후에도 계속해서 나옴….)
y∼N(Aμ+b,AΣA⊤)y \sim \mathcal{N}\left(A \mu+b, A \Sigma A^{\top}\right)

Bayes Filter

베이즈 필터의 입출력 요소를 간단하게 살펴보자.
주어지는 것 (Given)
•
관측치 요소들 z1:tz_{1: t} 과 Action 요소(외부) u1:tu_{1: t}
•
관측 모델 p(zt∣xt)p\left(z_t \mid x_t\right)
•
Action/motion 모델 p(zt∣xt,ut)p\left(z_t \mid x_t,u_t\right)
얻고 싶은 것 (Wanted)
•
동적 시스템의 state xtx_{t}
•
state에 대한 Posterior 확률 belief bel⁡(xt)=p(xt∣z1:t,u1:t)\operatorname{bel}\left(x_t\right)=p\left(x_t \mid z_{1: t}, u_{1: t}\right)이다.
베이즈 필터를 유도하기 전 알아야할 가정이 하나있다.

Markov Assumption

만약 우리가 state xx 에 대해 알고 있다면, 관측치 znz_n 은 z1,…,zn−1z_1, \ldots, z_{n-1} 과 독립이다.
우리가 완벽한 관측치와 프로세스 모델을 통해 추정을 하게 된다면, 모든 이전 정보가 현재의 스테이트에 반영되어 있을 것이므로 고려할 필요가 없다는 것이다.
p(x∣z1,…,zn)=p(zn∣x,z1,…,zn−1)p(x∣z1,…,zn−1)p(zn∣z1,…,zn−1)p\left(x \mid z_1, \ldots, z_n\right)=\frac{p\left(z_n \mid x, z_1, \ldots, z_{n-1}\right) p\left(x \mid z_1, \ldots, z_{n-1}\right)}{p\left(z_n \mid z_1, \ldots, z_{n-1}\right)}
이 조건을 이용한다면, 위 식을 아래의 식으로 변환 할 수 있다.
p(x∣z1,…,zn)=p(zn∣x)p(x∣z1,…,zn−1)p(zn∣z1,…,zn−1)=ηnp(zn∣x)p(x∣z1,…,zn−1)=η1:n∏i=1np(zi∣x)p(x)\begin{aligned}& p\left(x \mid z_1, \ldots, z_n\right)=\frac{p\left(z_n \mid x\right) p\left(x \mid z_1, \ldots, z_{n-1}\right)}{p\left(z_n \mid z_1, \ldots, z_{n-1}\right)} \\& \quad=\eta_n p\left(z_n \mid x\right) p\left(x \mid z_1, \ldots, z_{n-1}\right)=\eta_{1: n} \prod_{i=1}^n p\left(z_i \mid x\right) p(x)\end{aligned}
위에서 제시한, Markov Assumption, Marginalization, Bayes’ rule 등등을 이용하면 베이즈필터를 만들 준비는 끝난 것이다!
이에 대한 유도과정은 아래와 같다.
이를 통해 Bayes Filter는 두가지 단계로 나누어 표현할 수 있다.
•
Prediction step
◦
bel⁡‾(xt)=∫p(xt∣ut,xt−1)bel⁡(xt−1)dxt−1\overline{\operatorname{bel}}\left(x_t\right)=\int p\left(x_t \mid u_t, x_{t-1}\right) \operatorname{bel}\left(x_{t-1}\right) d x_{t-1}
•
Correction step
◦
bel⁡(xt)=ηp(zt∣xt)bel⁡‾(xt)\operatorname{bel}\left(x_t\right)=\eta p\left(z_t \mid x_t\right) \overline{\operatorname{bel}}\left(x_t\right)
Prediction step은 motion model로 생각할 수 있고, Correction step은 sensor 혹은 observation model을 의미하게 된다.
이에 대해 작성한 수도코드로 작성한 Bayes-filter 알고리즘은 아래와 같다.

Reference

Lecture 01-Introduction
MOBILE ROBOTICS: METHODS & ALGORITHMS - WINTER 2022 University of Michigan - NA 568/EECS 568/ROB 530 For slides, lecture notes, and example codes, see https://github.com/UMich-CURLY-teaching/UMich-ROB-530-public Theory and application of probabilistic and geometric techniques for autonomous mobile robotics. This course presents and critically examines contemporary algorithms for robot perception.
https://www.youtube.com/watch?v=pH4Pkmey2_E&list=PLdMorpQLjeXmbFaVku4JdjmQByHHqTd1F&index=1
UMich-ROB-530-public
UMich-CURLY-teaching
Made with