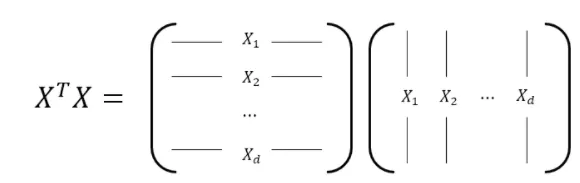
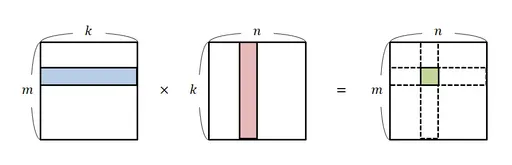
Matrix Multiplication을 표현하는 다양한 방법

첫번째 방법. 벡터의 inner product를 이용해 표현하는 방법

왼쪽에 제시된 행렬의 row vector와 오른쪽에 제시된 행렬의 column vector의 inner product한 값들의 집합으로써 정의하게 된다.

\left[\begin{array}{ll}1 & 6 \\3 & 4 \\5 & 2\end{array}\right]\left[\begin{array}{cc}1 & -1 \\2 & 1\end{array}\right]=\left[\begin{array}{cc}13 & 5 \\11 & 1 \\9 & -3\end{array}\right]

하나를 집어 예시로 들면, vector

\left[\begin{array}{lll}1 & 6 \end{array}\right]

과 vector

\left[\begin{array}{l}1 \\2 \end{array}\right]

의 inner product를 구해보면,

{1} \times1+{6} \times {2} = 13

의 값을 얻게 되고 이를 행렬의 한 element로 나타나게 되는것이다.

이러한 개념을 이용한 예시가 바로 Covariance Matrix이다.

이 행렬을 통해 데이터 간의 관계를 파악할수 있게 된다.

(SLAM에서는 각 센서간의 영향을 미치는 정도를 파악한다)

\left[\begin{array}{cccc}\operatorname{dot}\left(X_{1}, X_{1}\right) & \operatorname{dot}\left(X_{1}, X_{2}\right) & \cdots & \operatorname{dot}\left(X_{1}, X_{d}\right) \\\operatorname{dot}\left(X_{2}, X_{1}\right) & \operatorname{dot}\left(X_{2}, X_{2}\right) & \cdots & \operatorname{dot}\left(X_{2}, X_{d}\right) \\\vdots & \vdots & \ddots & \vdots \\\operatorname{dot}\left(X_{d}, X_{1}\right) & \operatorname{dot}\left(X_{d}, X_{2}\right) & \cdots & \operatorname{dot}\left(X_{d}, X_{d}\right)\end{array}\right]

왼쪽에 제시된 행렬의 column vector들을 bases로 생각하고, 오른쪽 행렬의 element들을 각 bases에 대한 coefficient로 생각하여 선형결합의 형태로 표현하는 방법

\left[\begin{array}{ccc}1 & 1 & 0 \\1 & 0 & 1 \\1 & -1 & 1\end{array}\right]\left[\begin{array}{l}1 \\2 \\3\end{array}\right]=\left[\begin{array}{l}1 \\1 \\1\end{array}\right] 1+\left[\begin{array}{c}1 \\0 \\-1\end{array}\right] 2+\left[\begin{array}{l}0 \\1 \\1\end{array}\right] 3

이러한 선형결합 형태로 표현하기 때문에 예전 포스트에서 다루었던 span, independence, Transformation 개념을 쉽게 이해할 수 있게 되었다.

앞서 다루었던 column vector의 형태와는 반대로, 오른쪽 행렬의 row vector를 bases로 생각하고, 왼쪽 행렬의 element를 coefficient로 생각하고 선형결합을 진행한다.

\left[\begin{array}{lll}1 & 2 & 3\end{array}\right]\left[\begin{array}{ccc}1 & 1 & 0 \\1 & 0 & 1 \\1 & -1 & 1\end{array}\right]=\begin{array}{c}1 \times\left[\begin{array}{lll}1 & 1 & 0\end{array}\right] \\+2 \times\left[\begin{array}{lll}1 & 0 & 1\end{array}\right] \\+3 \times\left[\begin{array}{lll}1 & -1 & 1\end{array}\right]\end{array}

(Rank-1) outer product는 아래와 같이 정의되는 방식을 말한다.

\left[\begin{array}{l}1 \\1 \\1\end{array}\right]\left[\begin{array}{lll}1 & 2 & 3\end{array}\right]=\left[\begin{array}{lll}1 & 2 & 3 \\1 & 2 & 3 \\1 & 2 & 3\end{array}\right]

위와 같은 곱셈 방식을 반영하여, 행렬간의 곱셈 또한 outer product의 합의 형태로 표현하는 방법이다.

\left[\begin{array}{cc}1 & 1 \\1 & -1 \\1 & 1\end{array}\right]\left[\begin{array}{lll}1 & 2 & 3 \\4 & 5 & 6\end{array}\right]=\left[\begin{array}{l}1 \\1 \\1\end{array}\right]\left[\begin{array}{lll}1 & 2 & 3\end{array}\right]+\left[\begin{array}{c}1 \\-1 \\1\end{array}\right]\left[\begin{array}{lll}4 & 5 & 6\end{array}\right]

=\left[\begin{array}{lll}1 & 2 & 3 \\1 & 2 & 3 \\1 & 2 & 3\end{array}\right]+\left[\begin{array}{ccc}4 & 5 & 6 \\-4 & -5 & -6 \\4 & 5 & 6\end{array}\right]

이러한 형태의 표현은 머신러닝 알고리즘에서 흔히 사용되는 표현 방식이며, multivariate Gaussian 분포를 가질 때 사용하는 Covariance matrix에도 이러한 형태로 분해하여 사용될 수 있다.