Linear Algebra
///
///
☔

PnP(Persepective-n-Point)에 대한 이해

생성일
2022/06/27 02:11
태그
PnP
DLT
P3P

PnP는 3D에서 2D로의 움직임을 추정하기 위한 방법입니다. 주어지는 것들은 다음과 같습니다.

•
nn 개의 3D 공간 상의 점
•
3D 점들이 2D 평면에 projection 되는 점의 위치
2D - 2D epipolar geometry에서는 8개 이상의 점들이 필요했다 (8-Point Algorithm). 하지만 PnP에서는 적어도 3개 이상의 3D-2D 매칭쌍들만 알면 카메라의 움직임을 추정할 수 있다.
쉽게 말해 PnP를 통해, epipolar constraint 없이, 더 적은 매칭쌍으로 , 더 좋은 추정 결과를 얻을 수 있다.
이러한 PnP 문제를 푸는 방법에는 DLT, EPnP, UPnP, P3P 등등이 있고, 이 모든 방법들은 non-linear Optimzation을 이용하여 iteratively 하게 푼다. 이러한 방법을 Bundle Adjustment라고 한다.
PnP를 푸는 알고리즘들을 몇 개만 살펴보자.

1. DLT(Direct Linear Transformation)

임의의 3차원 상의 점 PP 가 주어지고, 그것의 Homogeneous Coordinate P=(X,Y,Z,1)T\mathbf{P} = {(X,Y,Z,1)^T} 라고 하자, 이 3D Point가 이미지 평면 I1I_1 에 Projection되고, 이 때 Projection된 2D Point를 x1=(u1,v1,1)T\mathbf{x_1} = {(u_1,v_1,1)^T} 라고 하자. 이러한 가정이 주어진다면, 2D-3D 관계를 아래와 같은 수식을 나타낼 수 있다.
s(u1v11)=(t1t2t3t4t5t6t7t8t9t10t11t12)⏟[R∣t](XYZ1).s\left(\begin{array}{c}u_{1} \\v_{1} \\1\end{array}\right)=\underbrace{\left(\begin{array}{cccc}t_{1} & t_{2} & t_{3} & t_{4} \\t_{5} & t_{6} & t_{7} & t_{8} \\t_{9} & t_{10} & t_{11} & t_{12}\end{array}\right)}_{[\mathbf{R} \mid \mathbf{t}]}\left(\begin{array}{c}X \\Y \\Z \\1\end{array}\right) .
위의 식을 u1,v1u_1,v_1 에 대해 풀어 내면, 아래 처럼 나타낼 수 있다.
u1=t1X+t2Y+t3Z+t4t9X+t10Y+t11Z+t12,v1=t5X+t6Y+t7Z+t8t9X+t10Y+t11Z+t12u_{1}=\frac{t_{1} X+t_{2} Y+t_{3} Z+t_{4}}{t_{9} X+t_{10} Y+t_{11} Z+t_{12}}, \quad v_{1}=\frac{t_{5} X+t_{6} Y+t_{7} Z+t_{8}}{t_{9} X+t_{10} Y+t_{11} Z+t_{12}}
식 표현의 편의를 위해, TT 를 row vector의 형태로 만들면,
t1=(t1,t2,t3,t4)T,t2=(t5,t6,t7,t8)T,t3=(t9,t10,t11,t12)T\mathbf{t}_{1}=\left(t_{1}, t_{2}, t_{3}, t_{4}\right)^{T}, \mathbf{t}_{2}=\left(t_{5}, t_{6}, t_{7}, t_{8}\right)^{T}, \mathbf{t}_{3}=\left(t_{9}, t_{10}, t_{11}, t_{12}\right)^{T}
방금 구한 u1,v1u_1,v_1 에 대한 식을 변형하면 아래와 같은 식으로 정리할 수 있다.
t1TP−t3TPu1=0t2TP−t3TPv1=0\begin{gathered}\mathbf{t}_{1}^{T} \mathbf{P}-\mathbf{t}_{3}^{T} \mathbf{P} u_{1}=0 \\\mathbf{t}_{2}^{T} \mathbf{P}-\mathbf{t}_{3}^{T} \mathbf{P} v_{1}=0\end{gathered}
우리의 목표는 행렬 TT 의 원소들 t1,t2,....,t12t_1,t_2,....,t_{12} 를 구하는 것이 목적이다. 구하고자 하는 미지수는 12개인데, 매칭쌍 하나로는 2개의 방정식이 주어지므로, 적어도 6개의 매칭쌍이 필요하다는 것을 알 수 있다. N개의 매칭쌍이 주어진다면, 아래와 같은 연립방정식의 형태로 나타낼 수 있다. 이런 방식으로 Rotation, Translation을 구하는 방식을 DLT라고 한다.
(P1T0−u1P1T0P1T−v1P1T⋮⋮⋮PNT0−uNPNT0PNT−vNPNT)(t1t2t3)=0\left(\begin{array}{ccc}\mathbf{P}_{1}^{T} & 0 & -u_{1} \mathbf{P}_{1}^{T} \\0 & \mathbf{P}_{1}^{T} & -v_{1} \mathbf{P}_{1}^{T} \\\vdots & \vdots & \vdots \\\mathbf{P}_{N}^{T} & 0 & -u_{N} \mathbf{P}_{N}^{T} \\0 & \mathbf{P}_{N}^{T} & -v_{N} \mathbf{P}_{N}^{T}\end{array}\right)\left(\begin{array}{l}\mathbf{t}_{1} \\\mathbf{t}_{2} \\\mathbf{t}_{3}\end{array}\right)=0
일반적으로, 주어지는 매칭쌍은 6개를 훨씬 상회하는 경우가 대부분이다. 그렇다면 방정식의 개수가 미지수의 개수보다 많은 형태를 띄게 되고, 이는 Overdetermined equation이 된다. 따라서 이를 실제로 풀기 위해서는 SVD를 이용하여 Least Square solution을 찾아야 한다.
더불어, 일반적으로 SLAM을 진행하는데 있어서, Intrinsic Parameter KK 는 Calibration 과정을 통해 이미 알고 있다고 전제하고 위의 과정을 진행하게 된다. 물론 위의 과정을 통해 Intrinsic Parameter를 추정할 수도 있지만, 미지수가 늘어나는 만큼 결과또한 좋지 못하기 때문에, Calibration을 통해 미리 얻은 값을 가지고 DLT를 진행하게 된다.

2. P3P

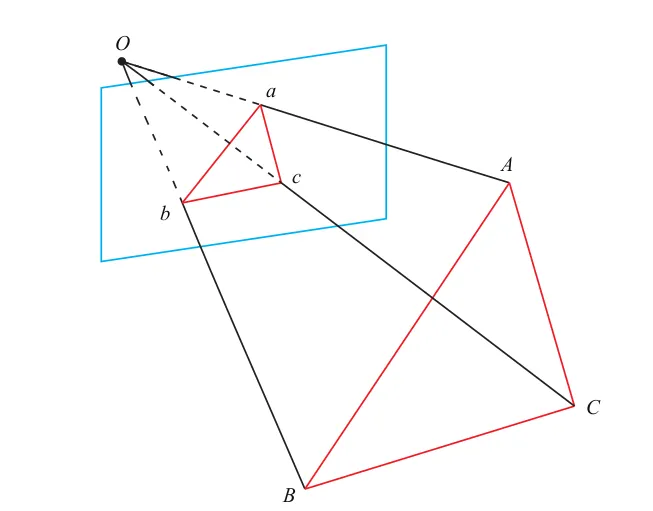
앞서 DLT 방법이 최소 6개 이상의 매칭쌍들을 이용했는데, P3P는 오직 3개의 매칭쌍을 필요로 한다. 주어진 3점 사이의 기하학적 관계를 이용하여 추정하게 되는데 아래와 같이 나타낼 수 있다.
3D point 점들이 A,B,CA,B,C 로 주어지고 그에 해당하는 (Projected) 2D Point를 a,b,ca,b,c 라고 하자.
위 그림에서 보면 알 수 있듯이, 삼각형 간의 관계를 아래와 같이 나타낼 수 있다.
△Oab−△OAB,△Obc−△OBC,△Oac−△OAC\triangle O a b-\triangle O A B, \quad \triangle O b c-\triangle O B C, \quad \triangle O a c-\triangle O A C
제2코사인법칙을 이용하여 각 삼각형 간의 식을 서술하자.
OA‾2+OB‾2−2⋅OA‾⋅OB‾⋅cos⁡⟨a,b⟩=AB‾2OB‾2+OC‾2−2⋅OB‾⋅OC‾⋅cos⁡⟨b,c⟩=BC‾2OA‾2+OC‾2−2⋅OA‾⋅OC‾⋅cos⁡⟨a,c⟩=AC‾2\begin{aligned}&\overline{O A}^{2}+\overline{O B}^{2}-2 \cdot \overline{O A} \cdot \overline{O B} \cdot \cos \langle a, b\rangle=\overline{A B}^{2} \\&\overline{O B}^{2}+\overline{O C}^{2}-2 \cdot \overline{O B} \cdot \overline{O C} \cdot \cos \langle b, c\rangle=\overline{B C}^{2} \\&\overline{O A}^{2}+\overline{O C}^{2}-2 \cdot \overline{O A} \cdot \overline{O C} \cdot \cos \langle a, c\rangle=\overline{A C}^{2}\end{aligned}
위의 3개의 식의 양변을 OC‾2\overline{O C}^{2} 로 나눠주고, x=OA‾/OC‾x=\overline{O A} / \overline{O C}, y=OB‾/OC‾y=\overline{O B} / \overline{O C} 로 치환하면, 아래와 같이 서술할 수 있다.
x2+y2−2⋅x⋅y⋅cos⁡⟨a,b⟩=AB‾2/OC‾2y2+12−2⋅y⋅cos⁡⟨b,c⟩=BC‾2/OC‾2x2+12−2⋅x⋅cos⁡⟨a,c⟩=AC‾2/OC‾2\begin{aligned}&x^{2}+y^{2}-2 \cdot x \cdot y \cdot \cos \langle a, b\rangle=\overline{A B}^{2} / \overline{O C}^{2} \\&y^{2}+1^{2}-2 \cdot y \cdot \cos \langle b, c\rangle=\overline{B C}^{2} / \overline{O C}^{2} \\&x^{2}+1^{2}-2 \cdot x \cdot \cos \langle a, c\rangle=\overline{A C}^{2} / \overline{O C}^{2}\end{aligned}
각 우변에 해당하는 것들을 v=AB‾2/OC‾2,u.v=BC‾2/OC‾2,w.v=AC‾2/OC‾2v=\overline{A B}^{2} / \overline{O C}^{2}, u . v=\overline{B C}^{2} / \overline{O C}^{2}, w .v=\overline{A C}^{2} / \overline{O C}^{2} 로 치환하고 위 식을 다시 쓰면
x2+y2−2⋅x⋅y⋅cos⁡⟨a,b⟩−v=0y2+12−2⋅y⋅cos⁡⟨b,c⟩−u.v=0x2+12−2⋅x⋅cos⁡⟨a,c⟩−w.v=0\\x^{2}+y^{2}-2 \cdot x \cdot y \cdot \cos \langle a, b\rangle-v=0 \\y^{2}+1^{2}-2 \cdot y \cdot \cos \langle b, c\rangle-u . v=0 \\x^{2}+1^{2}-2 \cdot x \cdot \cos \langle a, c\rangle-w . v=0
1번 째 식을 vv 에 관한 식을 만든 뒤, 아래 2,3번째 식에 넣어 정리하면 아래와 같은 x,yx,y 에 대한 방정식 2개를 얻을 수 있다.
(1−u)y2−ux2−2cos⁡⟨b,c⟩y+2uxycos⁡⟨a,b⟩+1=0(1−w)x2−wy2−2cos⁡⟨a,c⟩x+2wxycos⁡⟨a,b⟩+1=0\begin{aligned}&(1-u) y^{2}-u x^{2}-2 \cos \langle b, c\rangle y+2 u x y \cos \langle a, b\rangle+1=0 \\&(1-w) x^{2}-w y^{2}-2 \cos \langle a, c\rangle x+2 w x y \cos \langle a, b\rangle+1=0\end{aligned}
위의 식에서 cos⁡⟨a,b⟩,cos⁡⟨b,c⟩,cos⁡⟨a,c⟩\cos \langle a, b\rangle ,\cos \langle b, c\rangle, \cos \langle a, c\rangle 는 2D Point의 위치를 알고 있다는 가정에 의해 구할 수 있는 값이다. 또한 u=BC‾2/AB‾2,w=AC‾2/AB‾2u=\overline{B C}^{2} / \overline{A B}^{2}, w=\overline{A C}^{2} / \overline{A B}^{2} 의 경우 월드 좌표계에서 A,B,CA,B,C 의 좌표를 알고 있기 때문에 구할 수 있는 값이다. 2개의 방정식에 2개의 미지수이므로 x,yx,y 를 구할 수 있으며,
풀게 되면 4개의 가능한 x,yx,y 쌍이 나온다. (Essential Matrix를 구할 때도 4개의 쌍이 나왔단 것을 떠올리자.) 이 중에서 하나를 선택하기 위해 1개의 additional matching pair를 이용하여 최적의 x,yx,y 를 구한다.
x,yx,y 의 값을 구하게 되면, 카메라 좌표계에서의 3D Point A,B,CA,B,C 를 구할 수 있으며, 이를 통해 2D - 3D 문제를 3D - 3D pose estimation 문제로 바꿔 풀 수 있다. 흔히들 이러한 방법을 ICP라고 한다.
이러한 P3P도 단점이 존재한다. 3개의 데이터만 사용하기 때문에 더 적은 데이터를 요구하지만, 오히려
1.
오직 3개의 점만 가지고 추정하기 떄문에, 오히려 3개보다 많은 점들이 입력되면 추정하기 더 어렵다.
2.
추정에 사용되는 3개의 점이 노이즈나 잘못 매칭되었을 때 성능이 떨어질 수 있다.

Reference

slambook-en
gaoxiang12
Made with