슬램과 함께 춤을

Linear Algebra

5. Singular Value Decomposition

슬램과 함께 춤을

Linear Algebra

5. Singular Value Decomposition

📁

5. Singular Value Decomposition

태그

SVD

orthogonally diagonalizable

s.p.d

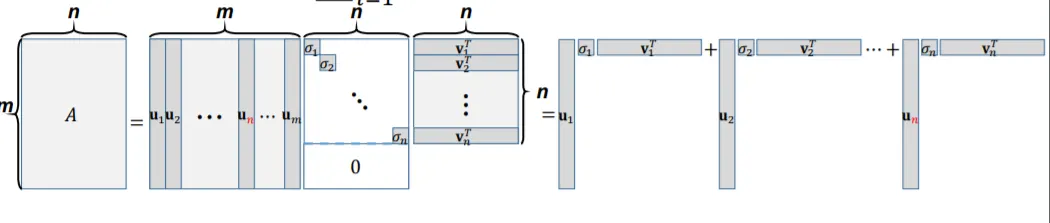
Singular Value Decomposition (SVD)

rectangular 행렬

A \in \mathbb{R}^{m \times n}

이 주어졌을 때, SVD는 아래와 같이 정의됩니다.

A=U \Sigma V^{T}=\sum_{i=1}^{n} \sigma_{i} \mathbf{u}_{i} \mathbf{v}_{i}^{T}, \quad \text { where } \sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{n}

이 때, SVD를 구성하는 각 행렬들은 아래와 같은 특징을 가집니다.

•

U∈Rm×mU \in \mathbb{R}^{m \times m}U∈Rm×m →  Col⁡A\operatorname{Col} AColA의 orthonormal basis에 해당하는 orthonormal column들로 이루어진 행렬

•

V∈Rn×nV \in \mathbb{R}^{n \times n}V∈Rn×n → Row⁡A\operatorname{Row} ARowA의 orthonormal basis에 해당하는 orthonormal column으로 이루어진 행렬

•

Σ∈Rm×n\Sigma \in \mathbb{R}^{m \times n}Σ∈Rm×n → σ1≥σ2≥⋯≥σmin⁡(m,n)\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{\min (m, n)}σ1​≥σ2​≥⋯≥σmin(m,n)​의 내림차순으로 정렬된 singular value값들을 entries로 가지는 diagonal matrix

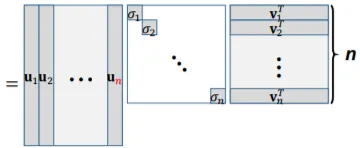
시각적으로 표현하면 아래와 같다.

이와 같이 표현할 경우,

\mathbf{U} \in \mathbb{R}^{m \times m} \rightarrow \mathbf{U}^{\prime} \in \mathbb{R}^{m \times n}

\mathbf{D} \in \mathbb{R}^{m \times n} \rightarrow \mathbf{D}^{\prime} \in \mathbb{R}^{n \times n}

로 축소되어 표현되며, 이를 Reduced form of SVD라고한다.

Another Perspective of SVD

앞서 배운 Gram-Schmidt orthogonalization을 활용하면, 쉽게 2개의 orthonormal basis 집합을 구할 수 있다.

\operatorname{Col} A

에 해당하는

\left\{\mathbf{u}_{1}, \ldots, \mathbf{u}_{n}\right\}

\operatorname{Row} A

에 해당하는

\left\{\mathbf{v}_{1}, \ldots, \mathbf{v}_{n}\right\}

그러나 이러한 orthonormal basis는 unique하지 않으며 여러가지 형태로 존재할 수 있다. 각 벡터

\mathbf{v_{i}, u_{i}}

는 아래와 같은 식을 만족한다.

A \mathbf{v}_{i}=\sigma_{i} \mathbf{u}_{i}, \quad \forall i=1, \ldots, n

앞서 다룬, EVD에서의

A \mathbf{x}=\lambda \mathbf{x}

와 굉장히 유사한 형태인것을 확인할 수 있다. 단지, EVD의 경우 양변의 orthonormal vector들의 dimension이 동일했던 것 대비, SVD에서는 양변의 orthonormal vector들의 dimension이 동일하지 않다.

Singular Values of an $m \times n$ Matrix

행렬

A

를

m \times n

행렬로 가정하면, 이 때,

A^{T}A

는 symmetric하기 때문에 orthogonally diagonalizable 합니다. (이전 챕터에서 다루었음)

\left\{\mathbf{v}_{1}, \ldots, \mathbf{v}_{n}\right\}

을 해당하는 eigenvector를 구성하는 orthonormal basis라고 가정한다면, 아래 조건을 만족합니다.

\left\|A \mathbf{v}_{i}\right\|^{2}=\left(A \mathbf{v}_{i}\right)^{T} A \mathbf{v}_{i}=\mathbf{v}_{i}^{T} A^{T} A \mathbf{v}_{i} \\\begin{array}{l} =\mathbf{v}_{i}^{T}\left(\lambda_{i} \mathbf{v}_{i}\right) \\ =\lambda_{i} \end{array}

행렬

A

의 singular value는 행렬

A^{T}A

의 eigenvector 값의 square root로 정의할 수 있다. 이는 벡터

A \mathbf{v}_{1}, \ldots, A \mathbf{v}_{n}

의 길이로도 해석할 수 있다.

\sigma_{i}=\sqrt{\lambda_{i}} \text { for } 1 \leq i \leq n

임의의 행렬 $A\in \mathbb{R}^{m \times n}$ 의 rank 구하는 방법

•

행렬 AAA를 row-reduction 한 후에 echelon form으로 만들어 pivot의 개수 구하기

•

행렬 ATAA^{T}AATA에 해당하는 eigenvalue, eigenvector를 구한 후 0이 아닌 rrr개의 singular values를 구하면, {Av1,…,Avr}\left\{A \mathbf{v}_{1}, \ldots, A \mathbf{v}_{r}\right\}{Av1​,…,Avr​}이 Col⁡A\operatorname{Col} AColA의 orthogonal basis가 되고,  rank⁡A=r\operatorname{rank} A=rrankA=r을 만족하게 된다.

몇몇의 경우에 한해서, 행렬

A

의 rank는 내부 원소의 조그마한 변화에도 민감하다. 컴퓨터로 row-reduction하는 경우 echelon form으로 변환하는 과정에서 round off-error가 발생하기 때문에 정확하게 되지 않게 된다. 따라서 첫번째 방법이 잘 동작하지 않게 된다. 실제 상황에서는 2번째 방법을 채택하여 큰 행렬에 대해서 rank를 구한다.

Computing SVD

먼저, eigendecomposition을 구하기 위해

AA^{T}, A^{T}A

를 형성한다.

\begin{array}{l}A A^{T}=U \Sigma V^{T} V \Sigma^{T} U^{T}=U \Sigma \Sigma^{T} U^{T}=U \Sigma^{2} U^{T} \\A^{T} A=V \Sigma^{T} U^{T} U \Sigma V^{T}=V \Sigma^{T} \Sigma U^{T}=V \Sigma^{2} V^{T}\end{array}

이 때,

AA^{T}, A^{T}A

는 symmetric이기 때문에 orthogonally diagonalizable 합니다. 이에 맞추어 eigendecomposition을 실행하면,

\begin{array}{c}S=U D U^{T}=\left[\begin{array}{llll}\mathbf{u}_{1} & \mathbf{u}_{2} & \cdots & \mathbf{u}_{n}\end{array}\right]\left[\begin{array}{cccc}\lambda_{1} & 0 & \cdots & 0 \\0 & \lambda_{2} & \ddots & \vdots \\\vdots & \ddots & \ddots & 0 \\0 & \cdots & 0 & \lambda_{n}\end{array}\right]\left[\begin{array}{c}\mathbf{u}_{1}^{T} \\\mathbf{u}_{2}^{T} \\\vdots \\\mathbf{u}_{n}^{T}\end{array}\right] \\=\lambda_{1} \mathbf{u}_{1} \mathbf{u}_{1}^{T}+\lambda_{2} \mathbf{u}_{2} \mathbf{u}_{2}^{T}+\cdots+\lambda_{n} \mathbf{u}_{n} \mathbf{u}_{n}^{T}\end{array} \\ \text { where } \lambda_{j}>0, \forall j=1, \cdots, n

각각의 term

\lambda_{i} \mathbf{u}_{j} \mathbf{u}_{j}^{T}

는

\mathbf{u}_{j}

에 의해 span되는 subspace로의 projection matrix로 해석할 수 있으며, 이 것은 eigenvalue

\lambda_{i}

로 Scale 됩니다.

이 때, 행렬

S

에 대한 특징을 2가지로 정리할 수 있습니다.

•

Symmetric → (AAT)T=AAT and (ATA)T=ATA\left(A A^{T}\right)^{T}=A A^{T} \text { and }\left(A^{T} A\right)^{T}=A^{T} A(AAT)T=AAT and (ATA)T=ATA

•

Positive-(semi-)definite → 아래 성질을 만족

\begin{array}{l}\mathbf{x}^{T} A A^{T} \mathbf{x}=\left(A^{T} \mathbf{x}\right)^{T}\left(A^{T} \mathbf{x}\right)=\left\|A^{T} \mathbf{x}\right\|^{2} \geq 0 \\\mathbf{x}^{T} A^{T} A \mathbf{x}=(A \mathbf{x})^{T}(A \mathbf{x})=\|A \mathbf{x}\|^{2} \geq 0\end{array}

위의 s.p.d 조건을 통해 항상 orthogonal한 eigenvector 행렬

U,V

를 찾을 수 있으며,

\Sigma^{2}

로 표현되는 eigenvalues는 항상 positive하다는 것을 알 수 있습니다!

정리하면, 임의의 rectangular matrix

\mathbf{A} \in \mathbb{R}^{m \times n}

에 대해 SVD는 항상 존재합니다. 이 행렬

A

를 가지고 만든 s.p.d matrix

S

는 항상 EVD 가능하며, SVD와 동일합니다.

실제 값으로 SVD 진행해보기

Reference

인공지능을 위한 선형대수 강좌소개 : edwith

인공지능을 위한 선형대수

Linear Algebra and Its Applications

Buy Linear Algebra and Its Applications on Amazon.com ✓ FREE SHIPPING on qualified orders

5. Singular Value Decomposition

Singular Value Decomposition (SVD)

Another Perspective of SVD

Singular Values of an m×nm \times nm×n Matrix

임의의 행렬 A∈Rm×nA\in \mathbb{R}^{m \times n}A∈Rm×n 의 rank 구하는 방법

Computing SVD

실제 값으로 SVD 진행해보기

Reference

Singular Values of an $m \times n$ Matrix

임의의 행렬 $A\in \mathbb{R}^{m \times n}$ 의 rank 구하는 방법