Linear Algebra
///
///
⛵

Epipolar Geometry Basics

생성일
2022/02/14 08:21
태그
epipole
epipolar line
epipolar axis
epipolar plane

Epipolar Geometry 과정

목표 : 첫 번째 이미지의 점에 해당하는 두 번째 이미지의 평면에 존재하는 점 X′′\mathcal{X}^{\prime\prime}를 찾기
주어진 것 : 첫 번째 이미지의 평면에 존재하는 점 X′\mathcal{X}^{\prime}
•
Image pairs의 기하학적인 관계를 표현하는 방법이다.
•
두 이미지 plane에 각각 같은 지점을 가리키는 점을 찾는 과정을 말한다.
•
straight-line preserving (Uncalibrated) camera를 가정하며, 찾는 공간이 2D (whole Image)에서 1D (Line)으로 줄어든다.

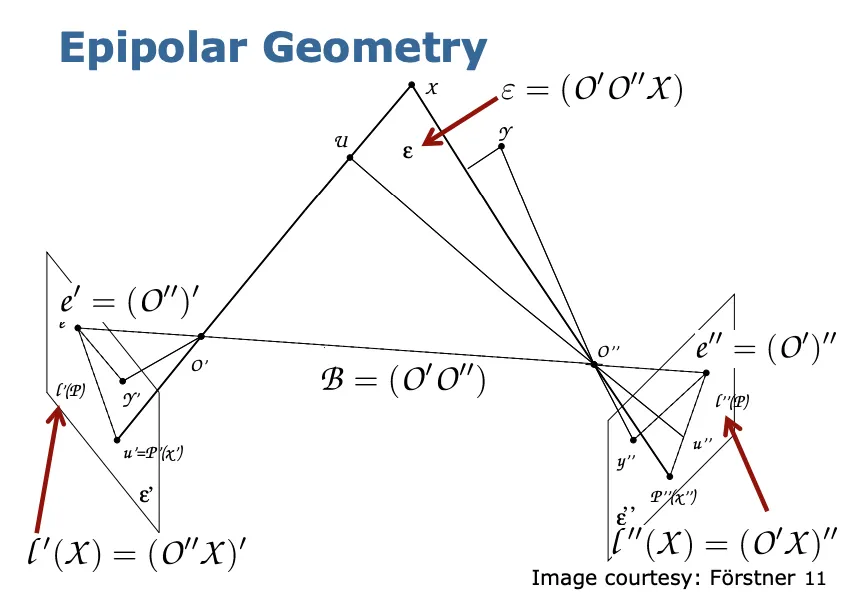
Epipolar Geometry를 구성하는 중요 요소들

1.
Epipolar axis B=(O′O′′)\mathcal{B}=\left(O^{\prime} O^{\prime \prime}\right) 2개의 카메라의 projection center를 잇는 직선을 의미합니다.
2.
Epipolar plane ε=(O′O′′X)\varepsilon=\left(O^{\prime} O^{\prime \prime} X\right) 2개의 projection center와 point x\mathbf{x} , 총 3개의 점으로 이루어지는 평면을 의미합니다.
3.
Epipoles e′=(O′′)′,e′′=(O′)′′e^{\prime}=\left(O^{\prime \prime}\right)^{\prime}, e^{\prime \prime}=\left(O^{\prime}\right)^{\prime \prime} 각각의 카메라의 Projection center가 다른 이미지 평면으로 투영될 때 생기는 점을 의미합니다. epipole들은 아래 조건을 만족합니다.
4.
Epipolar lines l′(X)=(O′′X)′,l′′(X)=(O′X)′′l^{\prime}(X)=\left(O^{\prime \prime} X\right)^{\prime}, l^{\prime \prime}(X)=\left(O^{\prime} X\right)^{\prime \prime} 각각의 직선 (O′′X)\left(O^{\prime \prime} X\right), (O′X)\left(O^{\prime} X\right)가 다른 이미지 평면으로 투영될 때 생기는 직선을 의미합니다.
epipole과 epipolar line은 아래 조건을 만족합니다.
e′=(O′O′′)∩ε′e′′=(O′O′′)∩ε′′e^{\prime}=\left(O^{\prime} O^{\prime \prime}\right) \cap \varepsilon^{\prime} \quad e^{\prime \prime}=\left(O^{\prime} O^{\prime \prime}\right) \cap \varepsilon^{\prime \prime}
l′(X)=ε∩ε′l′′(X)=ε∩ε′′l^{\prime}(X)=\varepsilon \cap \varepsilon^{\prime} \quad l^{\prime \prime}(X)=\varepsilon \cap \varepsilon^{\prime \prime}
1.
Epipolar plane ε\varepsilon 과 2번째 이미지 평면 ε′′\varepsilon^{\prime\prime}이 접하는 곳은 Epipolar lines l′′(X)l^{\prime\prime}(X)을 형성하고, x′x^{\prime}에 대응되는 점 x′′x^{\prime\prime}은 l′′(X)l^{\prime\prime}(X)위에 존재하게 됩니다. 찾는 공간을 2D에서 1D로 줄인 셈이 됩니다.

중요 요소들 구하는 방법

Projection matrix와 Fundamental matrix를 이용해 구할 것이다.

Epipolar axis

epipolar axis의 방향은 projection centers를 통해 바로 구해질 수 있다. 단, 방향만 알 수가 있다, 길이는 알 수가 없다!
b=XO′′−XO′\mathbf{b}=\boldsymbol{X}_{O^{\prime \prime}}-\boldsymbol{X}_{O^{\prime}}

Epipolar Lines

epipolar line에 있는 이미지 포인트 x′∈l′x^{\prime} \in l^{\prime} 에 대하여, 아래 식을 만족한다.
x′⊤l′=0\mathbf{x}^{\prime \top} \mathbf{l}^{\prime}=0
앞서 다룬 coplanarity constraint 조건을 활용해보면,
x′⊤Fx′′⏟l′=0l′=Fx′′\mathbf{x}^{\prime \top} \underbrace{F \mathbf{x}^{\prime \prime}}_{\mathbf{l}^{\prime}}=0 \\ \mathrm{l}^{\prime}=\mathrm{F} \mathbf{x}^{\prime \prime}
이미지 포인트 X′′∈l′′X^{\prime \prime} \in l^{\prime \prime} 에 대해서도, 똑같이 적용해보면,
l′′⊤x′′=0\mathrm{l}^{\prime \prime \top} \mathrm{x}^{\prime \prime}=0 \\
coplanarity constraint 조건 x′⊤Fx′′=0\mathbf{x}^{\prime \top} \mathrm{F} \mathbf{x}^{\prime \prime}=0 을 이용해보면, 아래의 직선을 구할수 있다 (1D space)
l′′⊤=x′⊤Fl′′=F⊤x′\mathrm{l}^{\prime \prime^{\top}}=\mathrm{x}^{\prime \top} \mathrm{F} \\ \mathrm{l}^{\prime \prime}=\mathrm{F}^{\top} \mathrm{x}^{\prime}

Epipoles

다른 이미지의 projection center를 현재 이미지 평면에 project시킨 것을 epipole 이라고 한다. 위에서 정의한 epipole의 정의를 식으로 표현하면 아래와 같다.
e′=P′XO′′e′′=P′′XO′\mathbf{e}^{\prime}=\mathrm{P}^{\prime} \mathbf{X}_{O^{\prime \prime}} \quad \mathbf{e}^{\prime \prime}=\mathrm{P}^{\prime \prime} \mathbf{X}_{O^{\prime}}
epipole들은 각 epipoar line위에 있기 때문에 아래 식 또한 만족한다.
∀l′:e′Tl′=0∀l′′:e′′Tl′′=0\forall \mathrm{l}^{\prime}: \mathrm{e}^{\prime \mathrm{T}} \mathrm{l}^{\prime}=0 \quad \forall \mathrm{l}^{\prime \prime}: \mathrm{e}^{\prime \prime \mathrm{T}} \mathrm{l}^{\prime \prime}=0
앞서 제시한 fundamental matrix FF를 이용하여 정의된 epipolar line을 결합시키면, 아래의 식을 만들 수 있다.
e′⊤Fx′′=0x′⊤Fe′′=0\mathbf{e}^{\prime \top} \mathrm{Fx}^{\prime \prime}=0 \quad\quad \mathrm{x}^{\prime \top} \mathrm{Fe}^{\prime \prime}=0
x′,x′′\mathbf{x}^{\prime },\mathbf{x}^{\prime \prime}이 zero-vector가 아니기 때문에, 아래 식을 만족해야만 하고
e′⊤F=0Fe′′=0e^{\prime \top} F=0 \quad F e^{\prime \prime}=0
위 식을 다시 정리하면,
F⊤e′=0Fe′′=0F^{\top} e^{\prime}=0 \quad F e^{\prime \prime}=0
위 꼴을 통해 각 행렬의 null space를 정의할 수 있게 된다.
null⁡(F⊤)=e′null⁡(F)=e′′\operatorname{null}\left(F^{\top}\right)=\mathbf{e}^{\prime} \quad \operatorname{null}(F)=\mathbf{e}^{\prime \prime}
F⊤e′=0Fe′′=0F^{\top} e^{\prime}=0 \quad F e^{\prime \prime}=0 식에서 알 수 있듯이, 각 epipole들은 F⊤,FF^{\top}, F를 Eigendecomposition하여 얻는 eigenvalue 중 0에 해당하는 eigenvector임을 알 수 있다. 이러한 분해를 통해 epipoles를 구할 수 있다.
Made with