Linear Algebra
///
///
👨🏽‍🏫

Chapter 9. Modern Recurrent Neural Network

생성일
2022/01/19 13:48
태그
RNN
GRU
LSTM
Seq2Seq
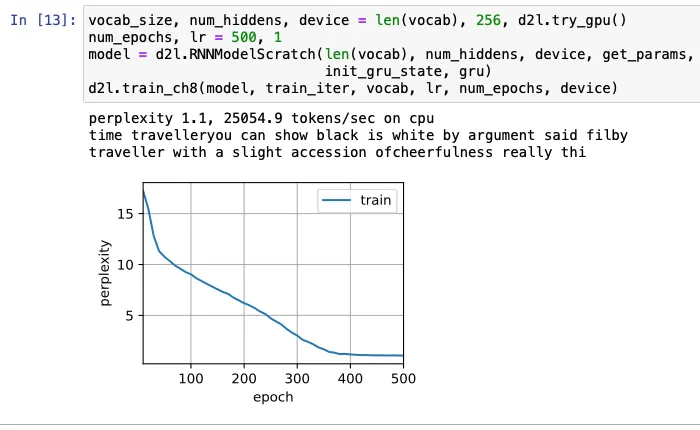
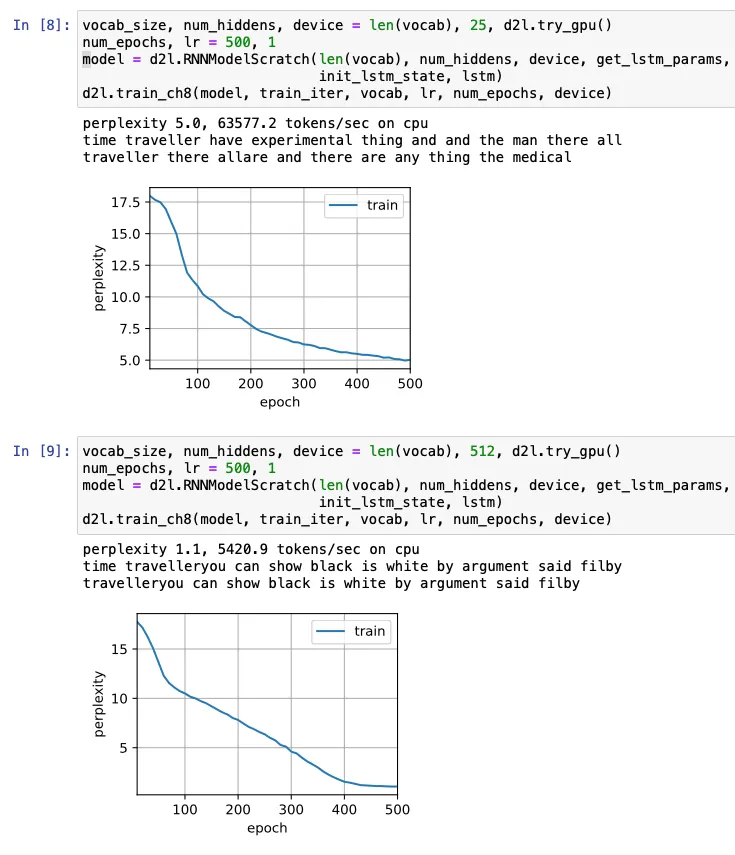
앞서 배운 단원에서 RNN의 기본적인 구조와 구현방법을 배워보았습니다. 하지만 RNN은 큰 문제가 있는데요, 바로 Short-term Memory 현상입니다. 비교적 이른 시간에 얻은 정보는 시간이 지남에 따라 잊혀지게 됩니다. 만약 중요한 정보가 초반부에 있었다면 언어모델, 기계번역의 성능이 안 좋아지게 됩니다.
backpropagation을 하면서 RNN은 gradient vanishing/exploding 문제를 겪게 됩니다. 따라서 학습이 잘 이루어지지 않게 되는데 이러한 대부분의 경우는 초반에 형성된 layers에서 많이 발생합니다. 이러한 layer들이 학습되지 않기 때문에 long sequence에 잘 대응하지 못하고, Long-term dependency(장기 의존성)문제를 가지게 됩니다.
앞서 배운 gradient clipping technique을 통해 gradient exploding 현상을 줄일 수는 있지만 더 적합한 방법은 sequence model을 더욱 더 복잡한 형태로 구현하는 것입니다.
이러한 복잡한 형태로 만드는 것이 바로 Gated RNN이라고 합니다, GRU, LSTM이 가장 대표적인 것들입니다. 두번째로 쓸 수 있는 테크닉은 MLP에서도 그랬듯, multiple hidden layers를 가지는 deep한 형태의 아키텍쳐를 구현할 수도 있습니다. 세번째로 forward , backprop 두 과정 모두에서 recurrent computation을 하는 형태를 가지는 bidirectional design을 할 수도 있습니다.

9.1  Gated Recurrent Units(GRU)

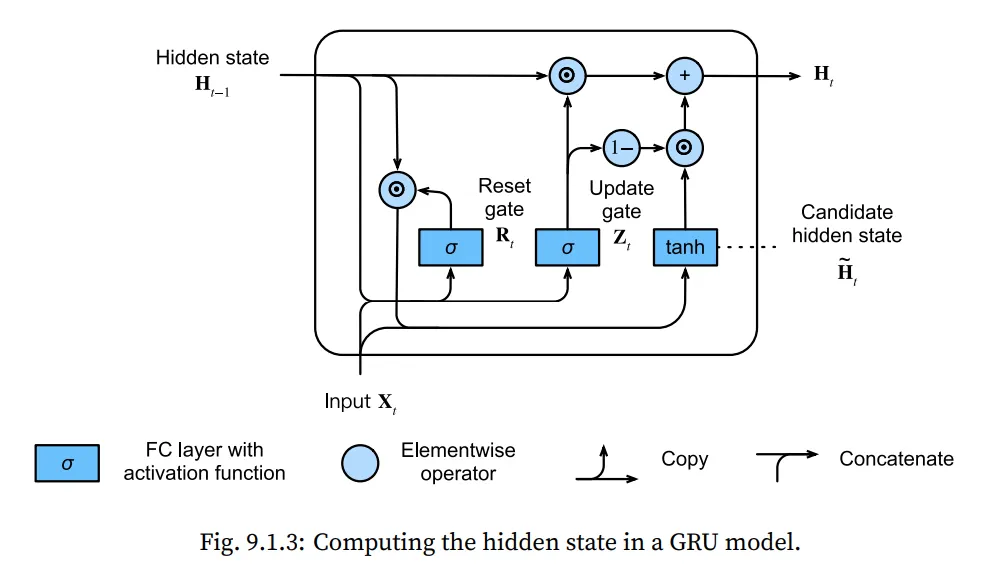
기본 RNN 모델과 GRU의 가장 큰 차이점은 hidden state에 대해서 gate를 사용한다는 것입니다. 게이트는 두가지로 나뉘어 집니다. Update 와 Reset 입니다!
Reset gate는 얼마나 이전의 state의 내용을 기억하고 싶은지를 컨트롤 할 수 있는 요소입니다. Update gate는 새로운 state의 내용을 old state의 내용으로 채울지를 컨트롤 하는 요소입니다.
이를 도식화 하면 아래와 같습니다.
입력이 Xt∈Rn×d\mathbf{X}_{t} \in \mathbb{R}^{n \times d} 로 주어지고, 이전 시간(t−1t-1) 에 대한 Hidden state Ht−1∈Rn×h\mathbf{H}_{t-1} \in \mathbb{R}^{n \times h} , reset gate를 Rt∈Rn×h\mathbf{R}_{t} \in \mathbb{R}^{n \times h} , update gate를 Zt∈Rn×h\mathbf{Z}_{t} \in \mathbb{R}^{n \times h} 로 정의 한 후, 수식을 전개하면 아래와 같다.
Rt=σ(XtWxr+Ht−1Whr+br)Zt=σ(XtWxz+Ht−1Whz+bz)\begin{array}{l}\mathbf{R}_{t}=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x r}+\mathbf{H}_{t-1} \mathbf{W}_{h r}+\mathbf{b}_{r}\right) \\\mathbf{Z}_{t}=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x z}+\mathbf{H}_{t-1} \mathbf{W}_{h z}+\mathbf{b}_{z}\right)\end{array}
이 때, Wxr,Wxz∈Rd×h\mathbf{W}_{x r}, \mathbf{W}_{x z} \in \mathbb{R}^{d \times h} 와 Whr,Whz∈Rh×h\mathbf{W}_{h r}, \mathbf{W}_{h z} \in \mathbb{R}^{h \times h}는 weight parameter로써 역할을 하고, br,bz∈R1×h\mathbf{b}_{r}, \mathbf{b}_{z} \in \mathbb{R}^{1 \times h} 는 biases로 역할을 합니다.
앞서 다룬 Vanila RNN의 hidden state 식을 다시 살펴보면 아래와 같은데, 이를 반영하여
Vanila RNN:Ht=ϕ(XtWxh+Ht−1Whh+bh).H~t=tanh⁡(XtWxh+(Rt⊙Ht−1)Whh+bh)\text Vanila\,RNN :\mathbf{H}_{t}=\phi\left(\mathbf{X}_{t} \mathbf{W}_{x h}+\mathbf{H}_{t-1} \mathbf{W}_{h h}+\mathbf{b}_{h}\right) \\ .\\\tilde{\mathbf{H}}_{t}=\tanh \left(\mathbf{X}_{t} \mathbf{W}_{x h}+\left(\mathbf{R}_{t} \odot \mathbf{H}_{t-1}\right) \mathbf{W}_{h h}+\mathbf{b}_{h}\right)
Wxh∈Rd×h\mathbf{W}_{x h} \in \mathbb{R}^{d \times h}, Whh∈Rh×h\mathbf{W}_{h h} \in \mathbb{R}^{h \times h} 가 또 다른 weight parameter, bh∈R1×h\mathbf{b}_{h} \in \mathbb{R}^{1 \times h} 가 biases가 됩니다. Rt\mathbf{R}_{t} 항을 통해 이전 state의 Ht−1\mathbf{H}_{t-1}의 영향력을 조절할 수 있게 됩니다. Rt\mathbf{R}_{t} 값이 1에 가까우면, Vanila RNN과 유사한 형태가 되고, Rt\mathbf{R}_{t} 값이 0에 가까우면, MLP의 형태를 가집니다. 따라서 이 term이 reset이라고 불리는 것입니다.
하지만 이 것은 Reset gate하고만 결합 된상태이고, update gate와는 아직 결합하지 않았기 때문에 완전한 형태가 아닙니다. 그래서 우리는 이것을 candidate Hidden state라고 부릅니다.
마지막으로, update gate Zt\mathbf{Z}_{t} 를 반영합니다. 이 게이트는 앞서 새롭게 만들어진 candidate hidden state Ht∈Rn×h\mathbf{H}_{t} \in \mathbb{R}^{n \times h} 와 예전 state Ht−1\mathbf{H}_{t-1} 중 어떤 것에 더 가중치를 둘지를 결정하는 역할을 합니다. 이를 수식으로 표현하면 아래와 같습니다.
Ht=Zt⊙Ht−1+(1−Zt)⊙H~t\mathbf{H}_{t}=\mathbf{Z}_{t} \odot \mathbf{H}_{t-1}+\left(1-\mathbf{Z}_{t}\right) \odot \tilde{\mathbf{H}}_{t}
Zt\mathbf{Z}_{t} 값이 1에 가까우면, old state를 유지하고, 입력 Xt\mathbf{X}_{t} 를 통해 들어온 정보가 무시됩니다. 반대로, Zt\mathbf{Z}_{t} 값이 0에 가까우면, candidate latent state H~t\tilde{\mathbf{H}}_{t} 의 영향을 많이 받게 됩니다.
이렇게 네트워크를 구성하게 되면 RNN 상에서의 vanishing gradient 문제를 해결할 수 있으며, 긴 시간 간격의 Sequence에도 잘 대응할 수 있게 됩니다. 예를 들어, Zt\mathbf{Z}_{t} 값이 모든 time step에 대하여, 1의 값을 가진다고 가정한다면, 각 time step의 old state의 정보가 subsequence의 길이에 상관없이 끝까지 유지될 수 있게 됩니다.

정리하면,

Reset gates는 주어진 sequence의 short-term 의존성을 조절하는데 사용하고, Update gates는 주어진 sequence의 long-term 의존성을 조절하는데 사용합니다!

9.2  Long Short-Term Memory(LSTM)

앞서 다루었던 GRU는 장기적인 정보를 보존하고, 단기적인 입력을 스킵할 수 있도록 하는 문제를 다루는데 효과적입니다. 이런 GRU와 비슷하지만 더 복잡한 desing을 갖고 있는 네트워크가 바로 LSTM입니다. 사실, LSTM이 GRU보다 20년 먼저 이 task를 다루었다고 합니다. (그럼 LSTM을 첫 챕터에 넣지...)
LSTM의 게이트는 GRU가 2개였던 것과 달리 총 3개의 gate를 가집니다.
1.
Foreget Gate → cell의 내용을 reset하는 역할 (GRU : reset gate)
2.
Input Gate → 언제 데이터를 cell로 읽어 들일지 정하는 역할
3.
Output Gate → cell로 부터 데이터를 읽는 역할
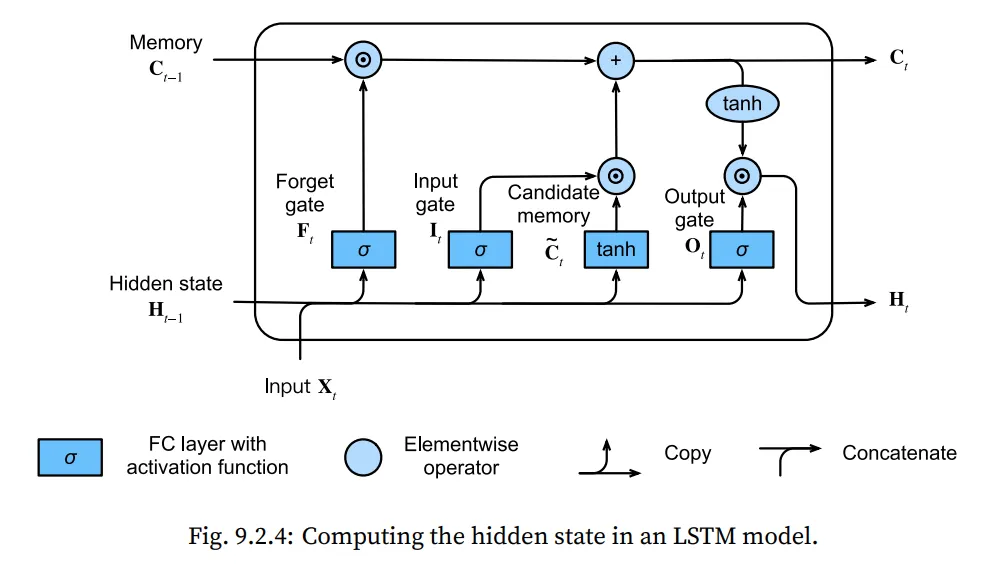
위 요소들을 통해 hidden state의 입력을 언제 기억하고 무시할지를 결정할 수 있게 됩니다.
구조를 보면 알 수 있지만, LSTM의 경우 memory cell, Hidden state 두 가지 부분으로 이루어져 있습니다!
먼저, Memory Cell의 구조를 살펴보면,
입력이 Xt∈Rn×d\mathbf{X}_{t} \in \mathbb{R}^{n \times d} 로 주어지고, 이전 시간(t−1t-1) 에 대한 Hidden state Ht−1∈Rn×h\mathbf{H}_{t-1} \in \mathbb{R}^{n \times h} , forget gate를 Ft∈Rn×h\mathbf{F}_{t} \in \mathbb{R}^{n \times h}, input gate를 It∈Rn×h\mathbf{I}_{t} \in \mathbb{R}^{n \times h}, output gate를 Ot∈Rn×h\mathbf{O}_{t} \in \mathbb{R}^{n \times h}로 정의 한 후, 수식을 전개하면 아래와 같다.
It=σ(XtWxi+Ht−1Whi+bi)Ft=σ(XtWxf+Ht−1Whf+bf)Ot=σ(XtWxo+Ht−1Who+bo)\begin{aligned}\mathbf{I}_{t} &=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x i}+\mathbf{H}_{t-1} \mathbf{W}_{h i}+\mathbf{b}_{i}\right) \\\mathbf{F}_{t} &=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x f}+\mathbf{H}_{t-1} \mathbf{W}_{h f}+\mathbf{b}_{f}\right) \\\mathbf{O}_{t} &=\sigma\left(\mathbf{X}_{t} \mathbf{W}_{x o}+\mathbf{H}_{t-1} \mathbf{W}_{h o}+\mathbf{b}_{o}\right)\end{aligned}
그리고 candidate memory cell C~t∈Rn×h\tilde{\mathbf{C}}_{t} \in \mathbb{R}^{n \times h} 는 위 게이트와 비슷하지만 Tanh를 쓴다는 점에서 다르다
C~t=tanh⁡(XtWxc+Ht−1Whc+bc)\tilde{\mathbf{C}}_{t}=\tanh \left(\mathbf{X}_{t} \mathbf{W}_{x c}+\mathbf{H}_{t-1} \mathbf{W}_{h c}+\mathbf{b}_{c}\right)
앞서 다룬 GRU에서 정보를 잊고 기억하는 역할을 하는 게이트를 소개해드렸습니다.
비슷하게 LSTM에도 그러한 역할을 하는 2개의 게이트가 존재합니다. Input Gate It\mathbf{I}_{t} 는 C~t\tilde{\mathbf{C}}_{t}와 연산을 함으로써, 얼마나 새로운 정보를 받아들일지 결정 합니다. forget Gate Ft\mathbf{F}_{t} 는 Ct−1{\mathbf{C}}_{t-1} 와 연산을 함으로써, old memory cell의 내용을 유지할지 결정합니다.
Ct=Ft⊙Ct−1+It⊙C~t\mathbf{C}_{t}=\mathbf{F}_{t} \odot \mathbf{C}_{t-1}+\mathbf{I}_{t} \odot \tilde{\mathbf{C}}_{t}
만약, forget gate 값이 1 이고 input gate 값이 0이라면, 과거 memory cell Ct−1\mathbf{C}_{t-1}이 계속 시간이 지나도 저장되게 됩니다. 이러한 design은 vanishing gradient 문제를 해결하는데 큰 도움이 되고, sequence가 긴 경우에도 도움을 줍니다.
Hidden State에 대해서 살펴보면,
Output gate와 memory cell의 tanh 된 형태의 곱으로 표현됩니다.
Ht=Ot⊙tanh⁡(Ct)\mathbf{H}_{t}=\mathbf{O}_{t} \odot \tanh \left(\mathbf{C}_{t}\right)
output gate 값이 1에 가까우면, 모든 메모리 정보를 예측하는데에 활용하지만, 반면에 0에 가까우면, 그냥 메모리상에 저장만 된채로 그냥 진행됩니다.

9.3 Deep Recurrent Neural Networks

복잡한 문제를 풀기 위해 linear model 에서 MLP로 바꿔 문제를 해결했던 것 처럼, single layer RNN은 한계가 존재합니다, 따라서 이번에도 Deep 한 형태로 layer들을 쌓아 보겠습니다.
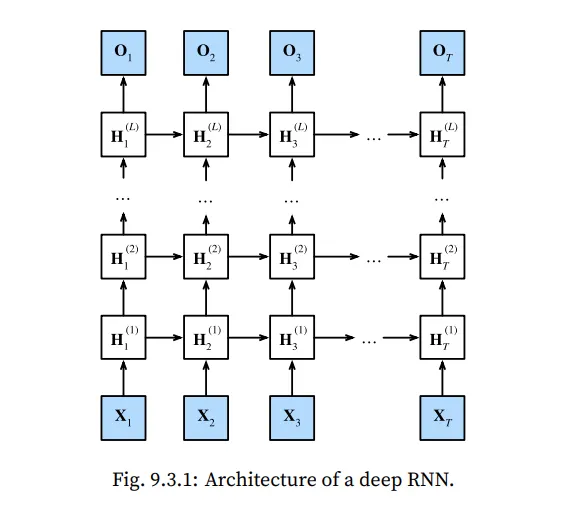
위에 제시한 모형은 LL hidden layers를 가지는 deep RNN 아키텍쳐 입니다. 그림에는 Vanila RNN model 의 형태로 제시되어 있지만, GRU, LSTM 모두 사용 가능 합니다.
hidden state는 아래와 같이 정의 됩니다.
Ht(l)=ϕl(Ht(l−1)Wxh(l)+Ht−1(l)Whh(l)+bh(l))\mathbf{H}_{t}^{(l)}=\phi_{l}\left(\mathbf{H}_{t}^{(l-1)} \mathbf{W}_{x h}^{(l)}+\mathbf{H}_{t-1}^{(l)} \mathbf{W}_{h h}^{(l)}+\mathbf{b}_{h}^{(l)}\right)
마지막에는, Output layer 계산이 마지막 hidden layer에 의해 행해집니다.
Ot=Ht(L)Whq+bq\mathbf{O}_{t}=\mathbf{H}_{t}^{(L)} \mathbf{W}_{h q}+\mathbf{b}_{q}

9.4 Bidirectional Recurrent Neural Networks

9.4.2  Bi directional Model

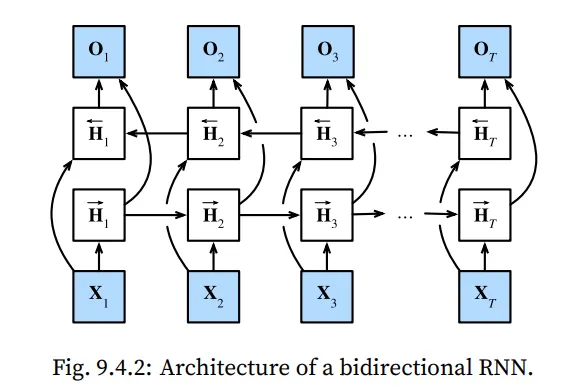
첫 번째 토큰으로 부터 시작하는 forward mode만 있는 RNN 보다는 맨 뒤 토큰부터 뒤에서부터 시작하는 것을 하나 더 추가합니다. 양방향 RNN은 정보를 역방향으로 전달하는 은닉 레이어를 추가해 보다 유연하게 처리한다.
위의 구조를 수식적으로 나타내면 아래와 같다.
forward hidden state H→t∈Rn×h\overrightarrow{\mathbf{H}}_{t} \in \mathbb{R}^{n \times h}와 backward hidden state H←t∈Rn×h\overleftarrow{\mathbf{H}}_{t} \in \mathbb{R}^{n \times h} 의 업데이트 과정은 다음과 같다.
H→t=ϕ(XtWxh(f)+H→t−1Whh(f)+bh(f))H←t=ϕ(XtWxh(b)+H←t+1Whh(b)+bh(b))\begin{array}{l}\overrightarrow{\mathbf{H}}_{t}=\phi\left(\mathbf{X}_{t} \mathbf{W}_{x h}^{(f)}+\overrightarrow{\mathbf{H}}_{t-1} \mathbf{W}_{h h}^{(f)}+\mathbf{b}_{h}^{(f)}\right) \\\overleftarrow{\mathbf{H}}_{t}=\phi\left(\mathbf{X}_{t} \mathbf{W}_{x h}^{(b)}+\overleftarrow{\mathbf{H}}_{t+1} \mathbf{W}_{h h}^{(b)}+\mathbf{b}_{h}^{(b)}\right)\end{array}
각각의 state를 구한뒤 이어주면 최종적인 hidden state Ht∈Rn×2h\mathbf{H}_{t} \in \mathbb{R}^{n \times 2 h}가 output layer에 들어가게 된다.
Ot=HtWhq+bq\mathbf{O}_{t}=\mathbf{H}_{t} \mathbf{W}_{h q}+\mathbf{b}_{q}
bi-directional RNN의 중요한 특징 중 하나는 현재의 것을 예측하기 위해 바로 과거의 정보와 미래의 정보를 둘 다 이용한다는 것입니다. 하지만 이러한 방법은 매우 느립니다. 그 이유는 forward propagation을 진행한다면 bi-directional한 layers에서 forward and backward 반복이 둘 다 필요합니다. 그리고 backpropagation은 forward propagation의 결과에 의존적입니다. 따라서 gradient를 구하려면 매우 긴 chain이 형성되어야 합니다.
이러한 특징들 때문에 실제로 Bi directional layer는 극히 일부 상황에서만 사용됩니다.

9.6 Encoder-Decoder Architecture

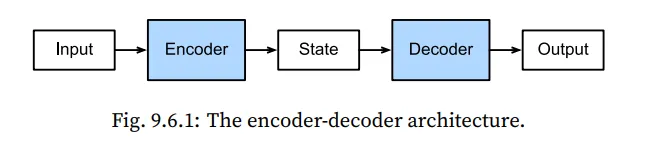
앞서 언급한대로, sequence transduction model에서 가장 큰 영역을 차지하는 task가 machine translation입니다. 이 task의 특징은 입력과 출력이 모두 길이가 변할수 있는 형태의 sequence라는 것입니다. 이러한 형태의 입출력을 다루기 위해, 우리는 2개의 요소로 구성된 아키텍쳐를 이용하게 되는데 이것이 바로 encoder와 decoder입니다.
Encoder는 가변 길이를 가지는 입력 sequence를 전달 받고 고정된 형태의 상태로 매핑합니다. 이후, 매핑된 정보를 다시 Decoder에 전달하여 가변 길이의 출력 sequence를 출력합니다.
Encoder와 Decoder는 각각 하나씩 RNN 아키텍쳐를 사용합니다. 따라서 두개의 RNN을 연결해서 사용하는 형태입니다.

9.7 Sequence to Sequence Learning

Sequence to Sequence Learning with Neural Networks
Deep Neural Networks (DNNs) are powerful models that have achieved excellent performance on difficult learning tasks. Although DNNs work well whenever large labeled training sets are available, they cannot be used to map sequences to sequences. In this paper, we present a general end-to-end approach to sequence learning that makes minimal assumptions on the sequence structure.
https://arxiv.org/abs/1409.3215
최근의 machine translate 방법은 딥러닝을 기반으로 동작합니다. 하지만 이러한 방법이 사용되기 전에는 전통적인 통계적인 방법을 통해 이루어져 왔습니다. 이번 단원에서 다루는 Sequence to Sequence learning 방법은 딥러닝을 이용한 machine translate 방법의 시초라 볼 수 있습니다. 이 논문 이후 attention, Transformer, GPT-1 등등... DNN 방법들이 학계를 지배하고 있습니다. 따라서 이 방법은 통계적인 방법과 딥러닝을 이용한 방법이 혼재되던 상황에서 딥러닝 기반으로 전환되었음을 알리는 기념비적인 논문이라고 할 수 있습니다.
이 방법은 end-to-end 방법으로 sequence to sequence 문제를 접근합니다.

Sequence to Sequence Learning의 특징

•
multilayered LSTM을 이용합니다 (4 layers)
•
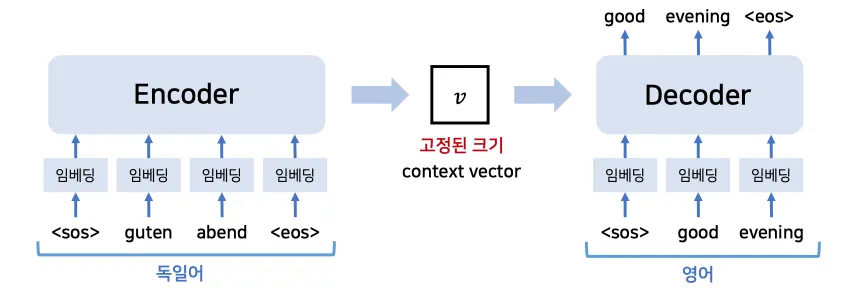
입력 sequence가 고정된 크기를 가지는 context vector로 매핑됩니다. (encode)
•
다른 쪽의 LSTM이 context vector를 입력 받아 target sequence를 만들어냅니다 (decode)
•
긴 문장에도 잘 동작합니다.
•
입력 sequence를 뒤집어서 입력함으로써 (reversed) LSTM의 성능을 향상시킵니다.
DNN은 강력한 성능을 보이지만, input과 target(output)의 dimension이 정해져 있어야만 했습니다. 이러한 경우 machine translation task에서 크게 힘을 쓰지 못합니다, 입력되는 문장과 출력되는 문장이 각 언어의 구조에 따라 단어의 개수가 달라지기 때문입니다.
예를 들어, 4개의 단어로 이루어진 한국어 문장이 있습니다.
(나는 너를 정말 사랑해 → I really love you ) 4 → 4 (모든 것은 그때부터 시작되었다 → Everything started then) 4 → 3
같은 4개의 단어로 이루어진 문장이라도 출력되는 문장의 개수는 다른 것을 알 수 있습니다. 이러한 문제를 해결하기 위해 LSTM 구조를 이용하게 됩니다.
인코딩 영역의 LSTM이 입력 시퀀스를 입력받은 뒤 크기가 큰 고정된 형태의 벡터 표현으로 변경됩니다. 그 후 디코딩 영역의 LSTM이 출력 시퀀스를 벡터로 부터 뽑아 냅니다.
임베딩을 하는 이유는?
예를 들어 독일어에서 자주 사용되는 단어가 2만개라고 가정하면 매 시간마다 2만 차원의 one-hot encoding으로 표현하고자 한다면 크기가 너무 커진다. 그래서 그 보다 작은 1~2천 차원의 정도의 작은 데이터로 표현될수 있도록 임베딩 layer를 둔다.
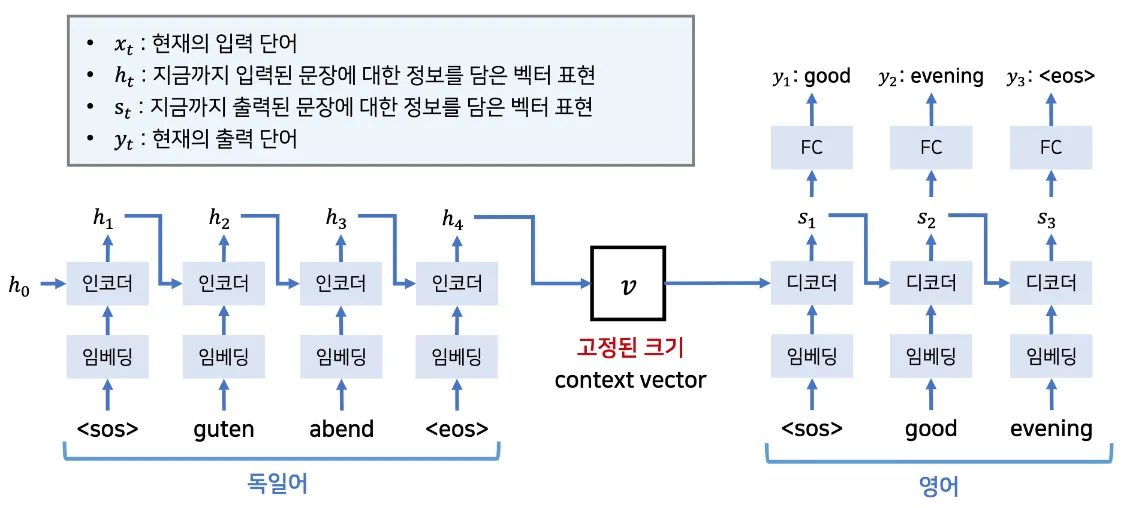
위의 모델을 수학적으로 표현하면 아래와 같습니다. 입력 (x1,…,xT)\left(x_{1}, \ldots, x_{T}\right)이 sequence의 형태로 주어지고, 출력을 (y1,…,yT)\left(y_{1}, \ldots, y_{T}\right)의 형태로 표현한다고 가정했을 때
ht=sigmoid⁡(Whxxt+Whhht−1)yt=Wyhht\begin{aligned}h_{t} &=\operatorname{sigmoid}\left(W^{\mathrm{hx}} x_{t}+W^{\mathrm{hh}} h_{t-1}\right) \\y_{t} &=W^{\mathrm{yh}} h_{t}\end{aligned}
궁극적으로 구하고자 하는 입력 시퀀스에 대한 출력 시퀀스의 확률 분포는 아래와 같이 나타내집니다.
p(y1,…,yT′∣x1,…,xT)=∏t=1T′p(yt∣v,y1,…,yt−1)p\left(y_{1}, \ldots, y_{T^{\prime}} \mid x_{1}, \ldots, x_{T}\right)=\prod_{t=1}^{T^{\prime}} p\left(y_{t} \mid v, y_{1}, \ldots, y_{t-1}\right)
이 때, 벡터 vv 가 입력 (x1,…,xT)\left(x_{1}, \ldots, x_{T}\right)이 고정된 크기로 전부 결합하여 나타내어진 것을 의미합니다.

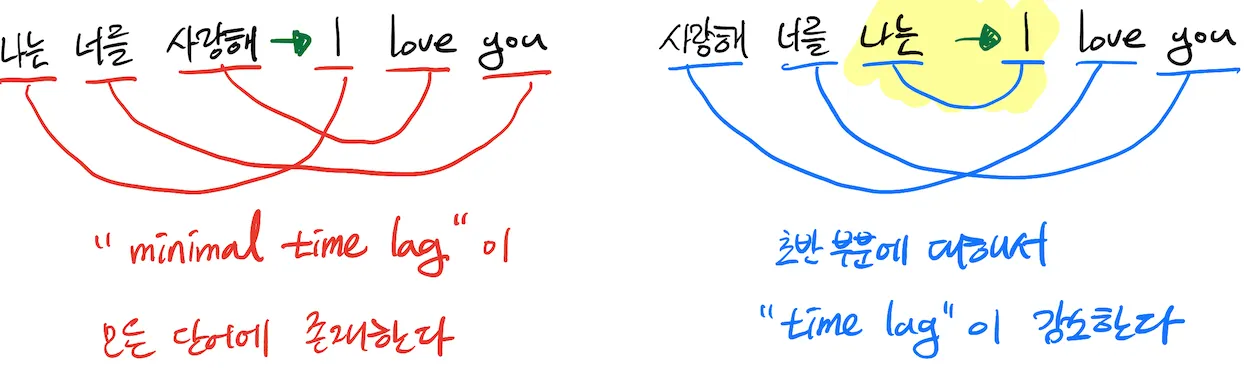
추가로, 성능 향상에 크게 기여한 부분이 있는데 바로 입력 문장을 반대로 입력하는 것입니다.

일반적으로 단어들 간의 종속성이 존재하는데, 보통 입력 문장의 각 단어들이 출력 문장과 거리가 멀게 위치하여 있습니다. 결과적으로 “minmal time lag” 이 발생하게 됩니다. 만약 입력 문장을 반대로 나열해 입력시키게 되면, 평균적인 단어들 간의 거리는 바뀌지 않겠지만, 입력 문장의 초반 단어들은 상당히 가깝게 위치하게 되고 time lag이 상당히 감소하게 됩니다. 일반적인 언어체계에서 앞쪽에 위치한 단어끼리 연관성이 높다는 것을 생각해 본다면, 성능 향상이 일어날 것을 알 수 있게 됩니다.

9.8 Beam Search

9.8.1 Greedy Search

output sequence의 임의의 time step t′t^{\prime}에서, 출력될 단어의 집합 Y\mathcal{Y} 중 가장 높은 조건부 확률을 가지는 토큰하나를 찾는 방법입니다. 수식으로 표현하면 아래와 같습니다.
yt′=argmax⁡y∈YP(y∣y1,…,yt′−1,c)y_{t^{\prime}}=\underset{y \in \mathcal{Y}}{\operatorname{argmax}} P\left(y \mid y_{1}, \ldots, y_{t^{\prime}-1}, \mathbf{c}\right)
각 타임 스탭마다 가장 높은 확률의 토큰을 뽑다보니 좋은 성능이 나올 것 같지만, 실제로 완성된 문장이 우리가 얻고자 하는 문장이라고 확신할 수는 없습니다.

예시 살펴보기

•
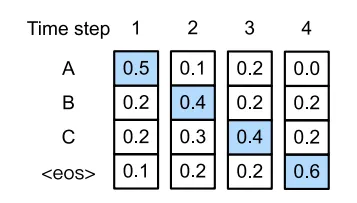
출력으로 나올 수 있는 4개의 토큰이 존재합니다 “A”, “B”, “C”, “<eos>”

첫번째 경우

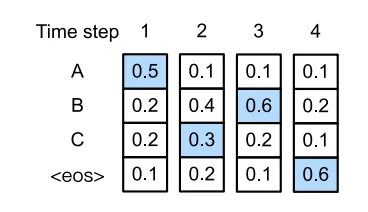
그리디 서치를 이용하는 경우 각각의 타임 스탭에서 제일 확률이 높은 것을 선택하게 되고, 차례차례 A → B → C → <eos> 의 순서로 선택하게 됩니다. 따라서 output sequence의 확률은 0.5×0.4×0.4×0.6=0.0480.5 \times 0.4 \times 0.4 \times 0.6=0.048 이 됩니다.

두번째 경우

두번째 예시를 살펴보면, 첫번째 경우와 다르게 2번째 스탭에서 확률이 0.3으로 2번째로 큰 확률 “B” 대신 “C” 를 선택합니다. 2번째 스텝에서 “C”를 선택함으로써 3번째 스텝에서의 토큰들의 확률이 변경된 것을 알 수 있습니다. 만약 이런 상황에서 3번째에 “C”를, 4번째에 “<eos>”를 선택하게 된다면, A → C → B → <eos> 순서이며, output sequence의 확률은 0.5×0.3×0.6×0.6=0.0540.5 \times 0.3 \times 0.6 \times 0.6=0.054 이 됩니다.
따라서, 이를 통해 그리디 서치 방법은 최적의 sequence가 아님을 알수 있습니다.

9.8.3 Beam Search

빔 서치는 그리디 서치를 향상시킨 버전으로 생각할 수 있습니다. 이러한 방법은 beam size kk 를 하이퍼파라미터로 사용할 수 있습니다.
첫번째 time step에서 가장 높은 확률을 가지는 kk 개의 토큰을 고릅니다. 두번째 time step에서 각각의 토큰들이 다시 그 자신을 기준으로 하는 kk 개의 토큰을 고릅니다. 이렇게 time step이 진행될 때 마다, 각 타임스탭에서 만들어지는 전체 경우의 수 k∣Y∣k|\mathcal{Y}| 중 가장 확률이 높은 kk개만을 골라 계속해서 문장이 끝날 때까지 반복하는 과정입니다.
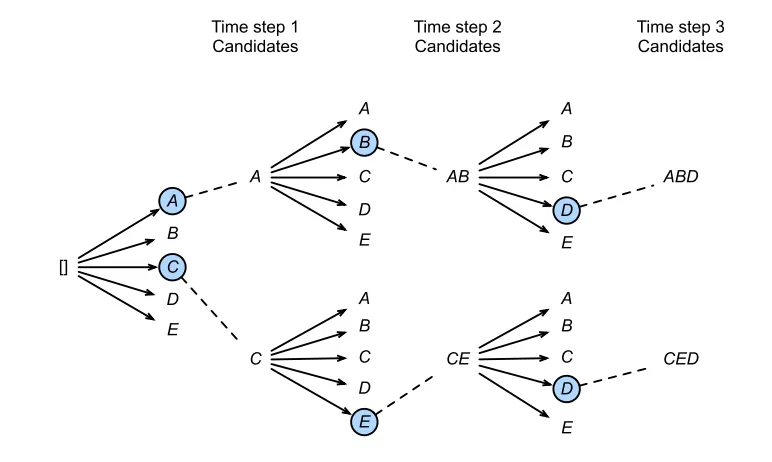
위의 경우를 살펴 보면, beam size = 2 , 출력 문장의 최대 길이 = 3 , 출력될 단어의 집합 Y={A,B,C,D,E}\mathcal{Y}=\{A, B, C, D, E\}일 때,
단, <eos> 제외. 아래의 수식은 위에서 설명한 토큰을 고르는 과정을 설명한 것이다.
P(y1∣c)P\left(y_{1} \mid \mathbf{c}\right) 중에서 가장 높은 확률을 가지는 토큰이 A,CA , C 이고, 2번째 타임스탭 때, 모든 y2∈Yy_{2} \in \mathcal{Y} 에 대해서 다시 조건부 확률을 구해보면,
P(A,y2∣c)=P(A∣c)P(y2∣A,c)P(C,y2∣c)=P(C∣c)P(y2∣C,c)\begin{array}{l}P\left(A, y_{2} \mid \mathbf{c}\right)=P(A \mid \mathbf{c}) P\left(y_{2} \mid A, \mathbf{c}\right) \\P\left(C, y_{2} \mid \mathbf{c}\right)=P(C \mid \mathbf{c}) P\left(y_{2} \mid C, \mathbf{c}\right)\end{array}
총 10개의 경우의 수 (AA → 5개, CC → 5개) 중 가장 큰 확률을 가지는 2가지만을 고르면 된다. 가장 큰 확률을 가지는 2가지가 P(A,B∣c) and P(C,E∣c)P(A, B \mid \mathbf{c}) \text { and } P(C, E \mid \mathbf{c}) 라고 한다면, 3번째 타임스탭에서
P(A,B,y3∣c)=P(A,B∣c)P(y3∣A,B,c)P(C,E,y3∣c)=P(C,E∣c)P(y3∣C,E,c)\begin{array}{l}P\left(A, B, y_{3} \mid \mathbf{c}\right)=P(A, B \mid \mathbf{c}) P\left(y_{3} \mid A, B, \mathbf{c}\right) \\P\left(C, E, y_{3} \mid \mathbf{c}\right)=P(C, E \mid \mathbf{c}) P\left(y_{3} \mid C, E, \mathbf{c}\right)\end{array}
이 확률들 중 P(A,B,D∣c) and P(C,E,D∣c)P(A, B, D \mid \mathbf{c}) \text { and } P(C, E, D \mid \mathbf{c}) 라고 한다면, 결과적으로 6개의 경우의 수를 얻을수 있게 된다.
 (i) A; (ii) C; (iii) A,B; (iv) C,E; (v) A,B,D; and (vi) C,E,D\text { (i) } A \text {; (ii) } C \text {; (iii) } A, B \text {; (iv) } C, E \text {; (v) } A, B, D \text {; and (vi) } C,E,D
마지막으로, 이 6개의 sequence로 부터 가장 확률이 높은 출력 시퀀스를 아래와 같은 방법으로 얻을수 있ek.
1Lαlog⁡P(y1,…,yL∣c)=1Lα∑t′=1Llog⁡P(yt′∣y1,…,yt′−1,c)\frac{1}{L^{\alpha}} \log P\left(y_{1}, \ldots, y_{L} \mid \mathbf{c}\right)=\frac{1}{L^{\alpha}} \sum_{t^{\prime}=1}^{L} \log P\left(y_{t^{\prime}} \mid y_{1}, \ldots, y_{t^{\prime}-1}, \mathbf{c}\right)
빔 서치 방법의 computational cost는 O(k∣Y∣T′)\mathcal{O}\left(k|\mathcal{Y}| T^{\prime}\right) 로 표현할 수 있고, 그리디 알고리즘은 kk 값이 1인 형태로 생각해 볼 수 있다. 식에서 알수 있듯이 beam size가 커지면 계산량이 증가하지만, 좀 더 자연스러운 문장을 구할수 있게 된다. 하지만 너무 많은 beam size를 이용하게 되면, 소수점인 수들을 여러번 곱하는 꼴이 되므로 값이 0에 가까워지게 된다. 이 문장이 정말 말이 안되는 문장인지 단순히 확률이 낮은지 구별 할 수 없게 된다.
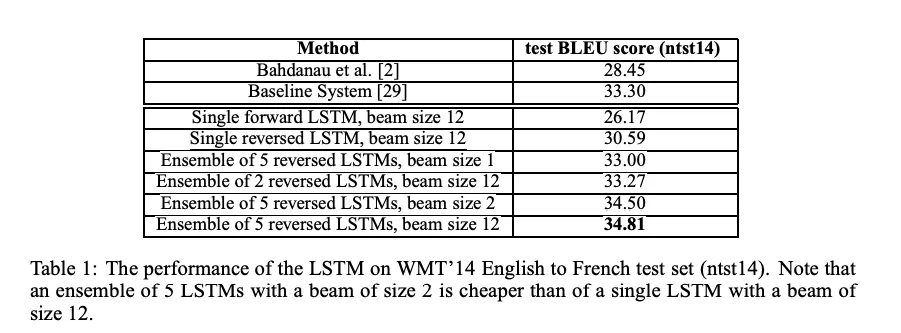
앞서 다룬 seq2seq 모델에서도 빔 사이즈를 증가시켜서 성능을 향상시켰다고 말하고 있습니다.

Implementation of Modern RNN

GRU

LSTM

Reference

Illustrated Guide to LSTM's and GRU's: A step by step explanation
Hi and welcome to an Illustrated Guide to Long Short-Term Memory (LSTM) and Gated Recurrent Units (GRU). I'm Michael, and I'm a Machine Learning Engineer in the AI voice assistant space. In this post, we'll start with the intuition behind LSTM 's and GRU's.
https://towardsdatascience.com/illustrated-guide-to-lstms-and-gru-s-a-step-by-step-explanation-44e9eb85bf21
[딥러닝 기계 번역] Seq2Seq: Sequence to Sequence Learning with Neural Networks (꼼꼼한 딥러닝 논문 리뷰와 코드 실습)
오늘의 딥러닝 논문 리뷰는 자연어 처리 쪽에서 매우 유명한 논문인 Seq2Seq입니다. Seq2Seq는 2014년 인공지능 분야 최우수 학회 중 하나인 NIPS에서 소개되었습니다. Seq2Seq는 현대의 기계 번역(machine translation) 기술들이 딥러닝 기반으로 전환...
https://www.youtube.com/watch?v=4DzKM0vgG1Y&list=PLRx0vPvlEmdADpce8aoBhNnDaaHQN1Typ&index=6
Dive into Deep Learning - Dive into Deep Learning 0.17.2 documentation
Authors Amazon Senior Scientist Amazon Scientist CMU Assistant Professor Amazon Senior Principal Scientist Amazon VP/Distinguished Scientist Vol.2 Chapter Authors Framework Adaptation Authors IIT Roorkee Student PyTorch Adaptation Akuity Founding Engineer TensorFlow Adaptation You can modify the code and tune hyperparameters to get instant feedback to accumulate practical experiences in deep learning.
https://d2l.ai/
Made with