Linear Algebra
///
///
🏓

Non-Linear Optimization 방법 비교하기

생성일
2022/02/21 01:51
태그
Newton-Raphson
Levenberg-Marquardt

오늘은 non-linear optimization을 해결하는 알고리즘 Gradient-Decent, Newton-Raphson (Gauss-Newton), Levenberg-Marquardt. 이 3가지를 수식적으로 비교해보고 어떤 강점을 가지는지 알아보도록 하겠다.

이러한 최적화 문제는 slam에서 계속 나오는 bundle adjustment, loop closure detection 등등 에서 필수적으로 사용되는 것이므로 꼭 익혀두자!
지금부터 소개할 방법들은 같은 목표를 가지고 있다. 바로 주어진 함수의 최솟값을 찾는 것이다.

Gradient Decent

Gradient descent 방법은 아래 식과 같이 어떤 초기값에서 시작해서 gradient의 반대 방향으로 계속 내려가다 보면 함수의 최소값을 찾을 수 있다는 방법이다. gradient descent 알고리즘의 식은 아래와 같이 표현된다.
xn+1=xn−λ∇f(xn)x_{n+1}=x_{n}-\lambda \nabla f\left(x_{n}\right)
이 알고리즘의 장점은 상당히 안정적으로 동작한다는 것이다. 어떠한 값의 분포가 주어져도 다른 방법대비 비교적 강건하게 동작한다.
단점은 λ\lambda값이 상수일 때, 만약 함수 값이 flat한 지역에서 최적화를 시도할 경우 ∇f(xn)\nabla f\left(x_{n}\right) 값이 0에 가깝기 때문에 step size가 작아지게 되어 최솟값 방향으로 이동하지 못하고 갇혀 버리게 된다. 반대로 너무 함수 값의 차이가 심해 절벽의 형태를 띄는 지역에서는 ∇f(xn)\nabla f\left(x_{n}\right)값이 너무 커져버려 step size가 커지게 되고 이에 따라 overshoot하여 최솟값에 도달하지 못하게 된다.
또 하나의 단점은 minimum에 도달하는 속도가 너무 느리다.

Newton-Raphson

Newton-Raphson 방법은 gradient와 curvature를 같이 고려하면서 해를 찾아가는 방식이다.
Newton-Raphson 알고리즘의 식은 아래와 같이 표현된다.
xn+1=xn−(∇2f(xn))−1∇f(xn)x_{n+1}=x_{n}-\left(\nabla^{2} f\left(x_{n}\right)\right)^{-1} \nabla f\left(x_{n}\right)
위의 식에서 사용되는 term중 가장 critical한 term이 바로 Hessian Matrix ∇2f(xn)\nabla^{2} f\left(x_{n}\right)이다.
Hessian Matrix HH를 풀어서 표현하면 아래와 같다.
H=∇2f(xn)=[∂2f∂x12∂2f∂x1∂x2⋯∂2f∂x1∂xn∂2f∂x2∂x1∂2f∂x22⋯∂2f∂x2∂xn⋮⋮⋱⋮∂2f∂xn∂x1∂2f∂xn∂x2⋯∂2f∂xn2]\boldsymbol{H}=\boldsymbol{\nabla}^{2} f\left(\boldsymbol{x}_{n}\right)=\left[\begin{array}{cccc}\frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\\frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\\vdots & \vdots & \ddots & \vdots \\\frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}}\end{array}\right]
이 방법의 가장 큰 특징은 Hessian Matrix ∇2f(xn)\nabla^{2} f\left(x_{n}\right)의 역행렬을 최솟값을 구하는 과정에서 사용한다는 것이다. 바로 이 부분이 장점이 되기도 하고 단점이 되기도 한다.
식을 보면, 이동하는 step size를 (gradient의 크기) / (Curvature의 크기)로 정한다는 것을 알 수 있다. 따라서, gradient가 큰 값을 갖더라도, curvature가 크면 (기울기 변화가 급격한 경우) 조금만 이동하게 되고, curvature가 작으면 (기울기 변화가 크지 않은 경우) 좀 더 많이 이동하면서 minimum을 찾아간다.
Newton-Raphson의 장점은 시작점만 잘 설정한다면 엄청나게 빠른 수렴 속도를 보여준다는 것이다. 그 이유는 수식에서 알 수 있지만, gradient ∇f(xn)\nabla f\left(x_{n}\right) 값 뿐 아니라, curvature ∇2f(xn)\nabla^{2} f\left(x_{n}\right) 정보도 고려하기 때문에 더 직접적인 루트로 이동할 수 있게 된다.
일반적으로 Curvature information이 주어지게 되면(함수가 곡선이 있는 형태라면) Gradient descent보다 Newton-Raphson이 더 빠르다.
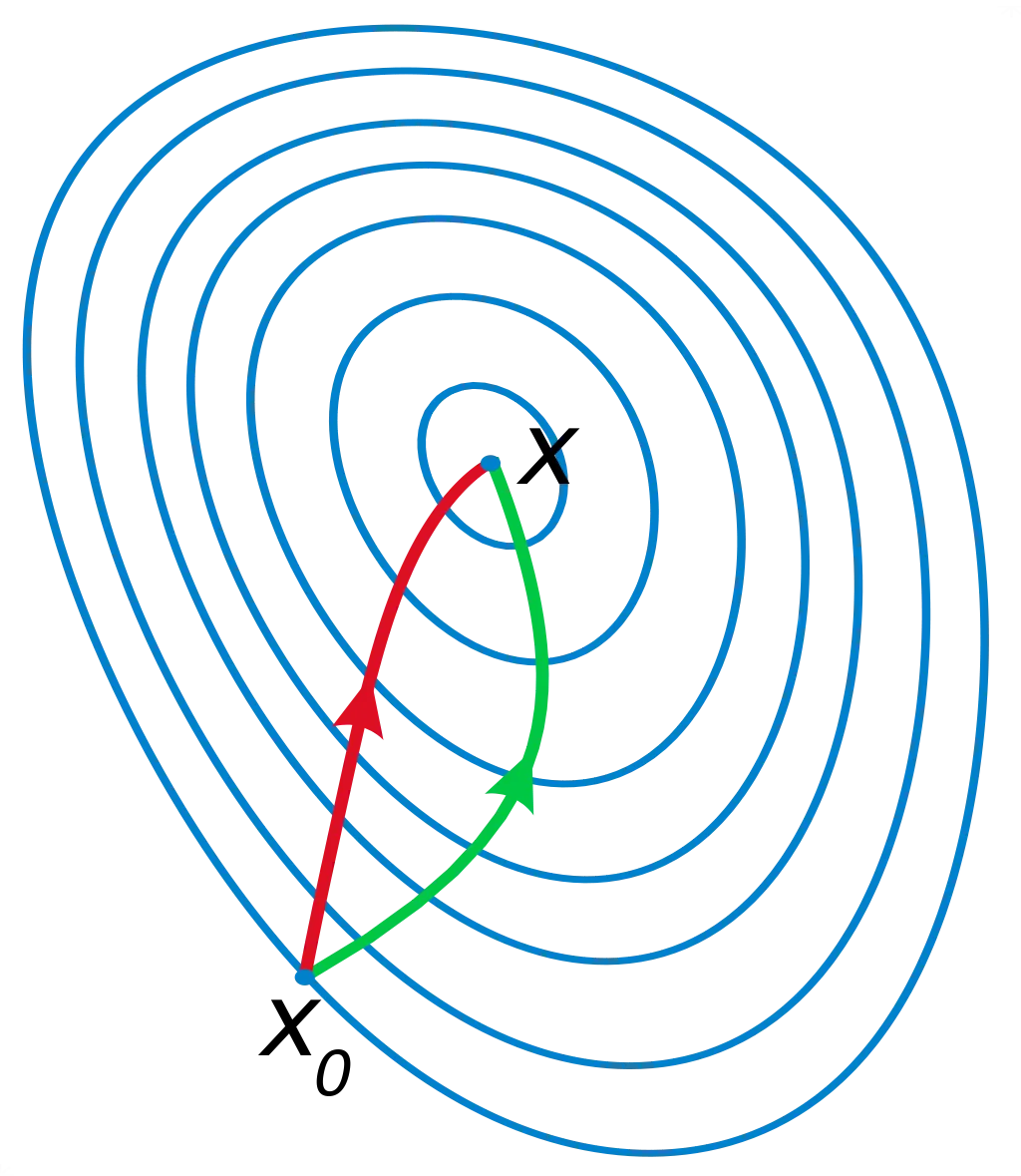
아래 그림은 빨간색으로 표시된 Newton-Raphson과 초록색으로 표시된 Gradient descent 방법이 수렴하는 것을 시각적으로 보여준다.
Newton-Raphson의 단점은 크게 4가지로 나뉜다.
•
시작점(Initial Guess)을 어떻게 설정하느냐에 따라 퍼포먼스가 크게 달라진다. minimun point에서 가까이 시작하면 시작할 수록 minima로 수렴할 확률이 올라간다. 반대로 말하면 시작점을 엉뚱한 곳에서 시작한다면 훨씬 느려지거나 수렴하지 못할 수도 있다.
•
행렬 HH가 positive definite 하지 않는 다면 값이 떨어지는 방향으로 이동하지 않을 수 있다.
•
행렬 HH가 역행렬이 존재 하지 않으면 알고리즘이 동작하지 않거나 발산할 수 있다.
•
행렬 HH를 구하고 역행렬까지 구하는 과정은 매우 시간이 많이 드는 연산 과정이다.
이러한 이유들 때문에 실제 데이터에 대해서 위의 알고리즘을 통해 최적화 하기는 쉽지 않다. 앞서 언급한 2가지 방법들에 대한 장점과 단점을 알아보았다. 그렇다면 이 2가지 방법의 장점만 쓸 수 없을까? 이를 위해 등장하는 방법이 바로 Levenberg-Marquardt 알고리즘이다.

Levenberg-Marquardt

Levenberg-Marquardt 방법은 ∇2f(xn)\nabla^{2} f\left(x_{n}\right)에 λI\lambda I항을 추가하여 발산의 가능성을 낮추고 안정적으로 동작하게 한 알고리즘이다. Levenberg-Marquardt 알고리즘의 식은 아래와 같이 표현된다.
xn+1=xn−(∇2f(xn)+λI)−1∇f(xn)x_{n+1}=x_{n}-\left(\nabla^{2} f\left(x_{n}\right)+\lambda I\right)^{-1} \nabla f\left(x_{n}\right)
수식을 살펴보면, Gradient descent와 Newton-Raphson의 식이 섞여있다는 것을 쉽게 알 수 있다.
λ→0\lambda \rightarrow 0에 가까운 값일 때에는 Newton-Raphson 알고리즘의 형태로 동작하게 되고, λ→∞\lambda \rightarrow \infty에 가까워지면 작은 step size를 가지는 GD 알고리즘의 형태로 동작한다. 또한 λ\lambda 값이 충분히 커지면, Hessian Matrix HH가 positive-definite하지 않더라도 행렬 H+λIH+\lambda I가 positive-definite 하게 되어 값이 떨어지는 방향으로 이동한다는 것을 보장할 수 있게 된다.
앞서 언급한 λ\lambda값은 고정된 값이 아니라, 매번 반복할 때마다 바뀌는 값이다. 현재 지점에서 안정적으로 minimum으로 수렴하고 있을 때에는 λ\lambda에 작은 값을 부여하고 Newton-Raphson방식으로 해를 찾고, minimum을 잘 찾지 못하고 있는 상황에서는 λ\lambda 값을 크게 주어 Gradient descent 방법으로 해를 찾게 된다.

Levenberg-Marquardt 알고리즘은 Gradient Decent보다 빠르고, Newton-Raphson 보다 안정적으로 동작합니다.

Reference

Levenberg-Marquardt Algorithm
Details of the Levenberg-Marquardt Algorithm and comparison between this method and the Gradient Descent and Newton-Raphson method are provided in this video...
https://www.youtube.com/watch?v=2ToL9zUR8ZI&list=PLjoIYgWzjQHJ5oE-JgNjYFetDMqS6eauy&index=18
함수최적화 기법 정리 (Levenberg-Marquardt 방법 등)
※ 참고로, 아래 글 보다는 최근에 올린 [기계학습] - 최적화 기법의 직관적 이해 를 먼저 읽어볼 것을 추천합니다. 그 이후에 아래 글을 읽어보시면 좋을 것 같습니다. ---------- 원래는 Levenberg-Marquardt 방법에 대한 내용을 쓰고자 했는데 글을 쓰다 보니 함수 최적화 기법들을 총 정리하는 글이 되고 말았습니다.
https://darkpgmr.tistory.com/142
Made with