Linear Algebra
///
///
🌄

Visual Feature Part 1: Computing Keypoints

생성일
2022/02/11 04:14
태그
KeyPoint
Corner
Harris
DoG
FAST
Keypoint는 이미지에서 특징점의 위치를 말합니다!
그렇다면 이러한 keypoint를 찾으려면 어떤 방법을 사용해야 할까요? 이번 포스트는 keypoint를 찾는 다양한 방법을 소개하고 수학적으로 어떻게 전개되는지 살펴보겠습니다.

Corner 검출하여 Keypoint 찾기

•
Corners는 주로 특징점이 된다.
•
translation, rotation, illumination(조명) 환경에 변화하지 않는다.
•
2개의 edge(갑작스러운 밝기 변화가 일어나는 곳)가 서로 수직하는 형태를 가진다.
위에서 언급했듯이, 엣지를 검출하기 위해서는 2개의 방향에 대한 밝기 변화를 찾을 필요가 있다. 이를 수식으로 표현하면 아래와 같다.
Pixel (x,y) 주변에 대한 Sum of Squared Differences of image(SSD) 를 구하는 것이다.
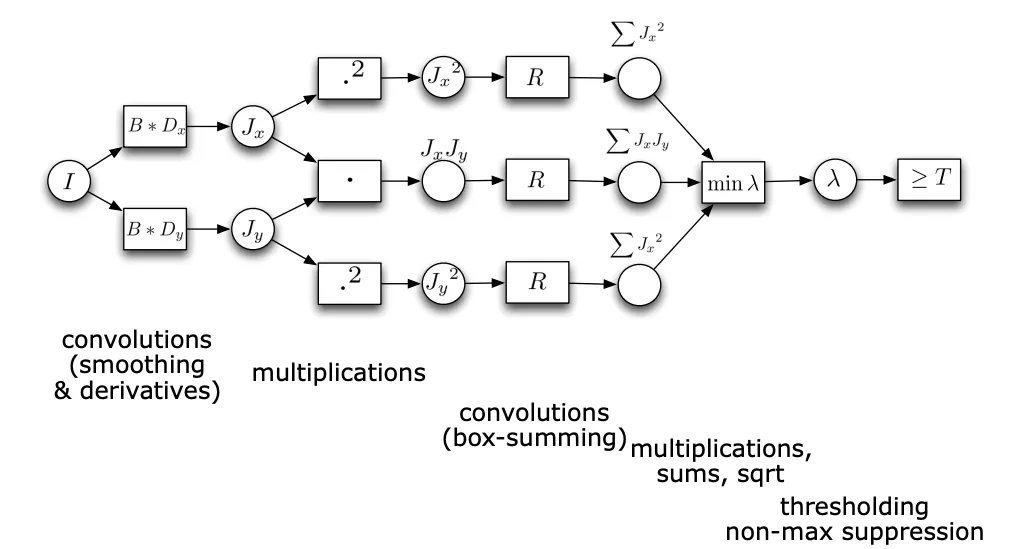
f(x,y)=∑(u,v)∈Wxy(I(u,v)−I(u+δu,v+δv))2f(x, y)=\sum_{(u, v) \in W_{x y}}(I(u, v)-I(u+\delta u, v+\delta v))^{2}
taylor expansion을 이용하면, 위의 델타항을 아래와 같이 치환할 수 있다. Jx,JyJ_{x} , J_{y} 는 행렬 II의 acobian이다.
I(u+δu,v+δv)≈I(u,v)+[JxJy][δuδv]I(u+\delta u, v+\delta v) \approx I(u, v)+\left[\begin{array}{ll}J_{x} \quad J_{y}\end{array}\right]\left[\begin{array}{l}\delta u \\\delta v\end{array}\right]
참고로, Jacobian을 구해 나갈 떄, Scharr 이나 Sobel과 같은 gradient kernel과 Convolution 하는 형태로 계산이 된다.
Jx2=(Dx∗I)2JxJy=(Dx∗I)(Dy∗I)Jy2=(Dy∗I)2\begin{aligned}J_{x}^{2} &=\left(D_{x} * I\right)^{2} \\J_{x} J_{y} &=\left(D_{x} * I\right)\left(D_{y} * I\right) \\J_{y}^{2} &=\left(D_{y} * I\right)^{2}\end{aligned}
이후 계속 식을 전개해 나가면,
f(x,y)≈∑(u,v)∈Wxy([Jx Jy][δuδv])2f(x, y) \approx \sum_{(u, v) \in W_{x y}}\left(\left[J_{x} \, J_{y}\right]\left[\begin{array}{l}\delta u \\\delta v\end{array}\right]\right)^{2}
f(x,y)≈∑(u,v)∈Wxy[δuδv]⊤[Jx2JxJyJxJyJy2][δuδv]f(x, y) \approx \sum_{(u, v) \in W_{x y}}\left[\begin{array}{l}\delta u \\\delta v\end{array}\right]^{\top}\left[\begin{array}{cc}J_{x}^{2} & J_{x} J_{y} \\J_{x} J_{y} & J_{y}^{2}\end{array}\right]\left[\begin{array}{l}\delta u \\\delta v\end{array}\right]
f(x,y)≈[δuδv]⊤[∑WJx2∑WJxJy∑WJyJx∑WJy2][δuδv]f(x, y) \approx\left[\begin{array}{c}\delta u \\\delta v\end{array}\right]^{\top}\left[\begin{array}{cc}\sum_{W} J_{x}^{2} & \sum_{W} J_{x} J_{y} \\\sum_{W} J_{y} J_{x} & \sum_{W} J_{y}^{2}\end{array}\right]\left[\begin{array}{l}\delta u \\\delta v\end{array}\right]

Structure Matrix

•
이 행렬을 통해 edge와 corners를 찾게 된다.
•
특정 지역의 이미지의 intensity의 변화 정도를 판단 할 수 있게 해준다.
•
행렬 MM 의 diagonal 성분을 통해 특정 방향의 gradient를 판단할 수 있다.
M=[∑WJx2∑WJxJy∑WJyJx∑WJy2]M=\left[\begin{array}{cc}\sum_{W} J_{x}^{2} & \sum_{W} J_{x} J_{y} \\\sum_{W} J_{y} J_{x} & \sum_{W} J_{y}^{2}\end{array}\right]
위와 같이 구한 행렬 MM을 eigen decomposition을 이용하여 아래와 같이 분해할 수 있고,
[δuδv]M[δuδv]= const \left[\begin{array}{ll}\delta u & \delta v\end{array}\right] M\left[\begin{array}{l}\delta u \\\delta v\end{array}\right]=\text { const }
[δuδv]R−1[λ100λ2]R[δuδv]= const \left[\begin{array}{ll}\delta u & \delta v\end{array}\right] R^{-1}\left[\begin{array}{cc}\lambda_{1} & 0 \\0 & \lambda_{2}\end{array}\right] R\left[\begin{array}{l}\delta u \\\delta v\end{array}\right]=\text { const }
이 때 eigenvalue λ1,λ2 \lambda_{1},\lambda_{2} 값이 모두 크다면 두 방향의 변화량이 크다는 것을 알수 있습니다.
위에서 제시한 방법을 이용해 corner detect를 하는 여러 가지 방법들이 존재합니다. 다만, 이러한 방법들이 소개되었을 때에는 실제 eigenvalue 값을 구하기엔 컴퓨터 성능이 좋지 않았던 상황이어서, Trace, determinant 를 이용해 값을 구하고 연산량을 줄였습니다.

(1) Harris Corner Criterion

가장 유명한 코너 디텍션 방법인것 같다. trace⁡(M)\operatorname{trace}(M)은 행렬 MM의 main diagonal 성분의 합을 의미한다.
R=det⁡(M)−k(trace⁡(M))2=λ1λ2−k(λ1+λ2)2\begin{aligned}R &=\operatorname{det}(M)-k(\operatorname{trace}(M))^{2} \\&=\lambda_{1} \lambda_{2}-k\left(\lambda_{1}+\lambda_{2}\right)^{2}\end{aligned}
∣R∣≈0⇒λ1≈λ2≈0: flat region R<0⇒λ1≫λ2 or λ2≫λ1: edge R≫0⇒λ1≈λ2≫0: corner \begin{array}{l}|R| \approx 0 \Rightarrow \lambda_{1} \approx \lambda_{2} \approx 0: \text { flat region } \\R<0 \Rightarrow \lambda_{1} \gg \lambda_{2} \text { or } \lambda_{2} \gg \lambda_{1}: \text { edge } \\R \gg 0 \Rightarrow \lambda_{1} \approx \lambda_{2} \gg 0: \text { corner }\end{array}

(2) Shi - Tomasi Corner Detector

코너라고 판단할 수 있는 최소한의 eigenvalue Threshold를 설정하여 각 eigenvalue가 이 값보다 클 때에만 코너로 취급한다.
대부분의 라이브러리에서 이 방법을 기본 corner detector로 사용한다. (openCV)
λmin⁡(M)=trace⁡(M)2−12(trace⁡(M))2−4det⁡(M)\lambda_{\min }(M)=\frac{\operatorname{trace}(M)}{2}-\frac{1}{2} \sqrt{(\operatorname{trace}(M))^{2}-4 \operatorname{det}(M)}
λmin⁡(M)≥T: corner \lambda_{\min }(M) \geq T: \text { corner }

(3) Forstner Operator

•
Harris Corner Detector와 유사한 구조를 가지고 있다.
•
행렬 MM 대신 M−1M^{-1}를 사용한다.
•
sub-pixel estimation을 이용한다.

Non-Maximum Suppression

harris corner의 경우 RR 값, shi-Tomasi의 경우 λmin⁡\lambda_{\min }을 사용한 것처럼, local region에서 가장 큰 값을 제외한 나머지를 버리는 방식을 말합니다.
아래 예시의 경우, 같은 corner를 발견했더라도, gradient의 개수가 가장 많은 3번째 경우가 feature로 선정됩니다!
corner dectection을 이용해 feature detect하는 3가지 방법을 알아보았다. 앞서 해온 과정을 도식화하면 아래와 같다.

다른 방법 소개

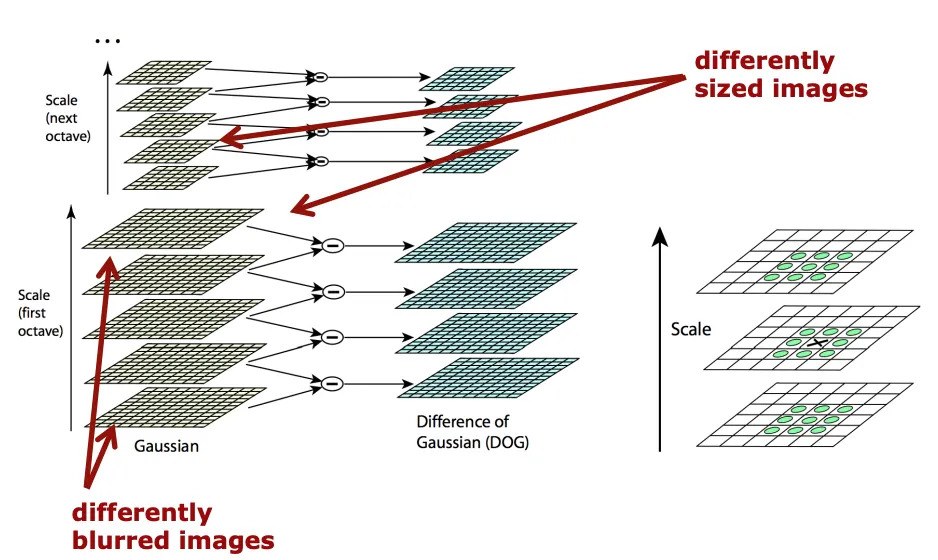
(4) Difference of Gaussians

기존의 harris-corner 방법의 경우, 영상의 스케일 변화에 민감한 성질을 가집니다, 이에 대응하여 DoG 방법은 이미지 내에서 코너를 찾을 뿐 아니라 스케일 변화에 민감하지 않은 코너까지 찾는 알고리즘입니다.

Scale-Invarient Corner detection

scale에 불변인 특징점이라는 것은 입력 이미지의 스케일이 어떠한 형태로 주어지더라도 해당 특징점을 찾을 수 있다는 것을 말합니다. 예를 들어 이미지 II가 주어졌을 때, 이 이미지를 단계적으로 축소하여 스케일이 다른 이미지들을 만듭니다. 이러한 이미지들을 모아놓은 것을 image pyramid라고 합니다. 이 때 각 스케일에 해당하는 이미지들의 코너를 검출하게 됩니다. (locally distinct → 코너성 극대, 임계값 이상). 따라서 각 스케일 이미지 마다 corner point가 검출되게 되고, 동일한 지점이 여러 이미지 스케일에 걸쳐 검출이 되면, 스케일 축에 대해서도 코너성이 극대인 점을 찾으면 됩니다. (이미지 상에서의 코너점 + 스케일 비교해서 코너점)

scale은 이미지의 크기가 아니다

이미지의 크기는 pixel 수, width, height 크기를 의미하지만,scale이 의미하는 것은 이미지의 detail입니다. scale이 크다는 것은 사물을 넓은 시야에서 바라 본다는 것을 의미합니다. 따라서 이미지의 크기를 축소시키면 detail을 잃게 됩니다. 이에 추가하여 크기는 동일하더라도 이미지가 bluring 된다면 detail을 잃게 됩니다.
•
이미지의 크기를 축소 ⇒ detail 잃는다 ⇒ scale이 크다
•
이미지를 블러링 한다 ⇒ detail 잃는다 ⇒ scale이 크다
특징점을 추출하는 기본적인 원리는 위의 제시된 방법과 동일하지만, 여기선 laplacian을 이용합니다. (라플라시안은 이미지 밝기 변화에 대한 2차 미분값을 나타내며, 변화가 일정한 곳은 0에 가까운 값을 가지고, 변화가 큰 곳에서는 높은 값을 갖게 됩니다.)
laplacian을 직접 계산하는 것은 속도가 너무 느리기 때문에 이 대신 DoG를 이용하게 됩니다. 입력 이미지에 가우시안 필터를 적용시켜 (각각 다른 σ\sigma를 주어 블러 정도를 다르게 한다) 블러링 시킨 후 인접한 이미지들 간의 차를 구하는 것을 말합니다.
이렇게 얻어지는 DoG 피라미드에서 극대/극소 점이 특징점이 된다.

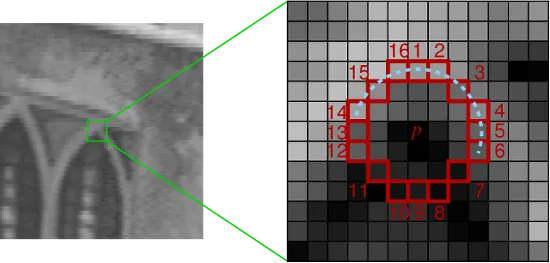
(5)FAST

FAST에선느 어떤 점 pp가 코너인지 아닌지를 밝히기 위해 점 pp를 중심으로 하는 반지름 3인 원을 구성하는 16개 픽셀 값들을 보고 결정하는 방법입니다. pp보다 threshold이상 밝은 픽셀 들이 n개 이상 연속되거나 어두운 픽셀들이 n개 이상 연속되어 있으면 코너로 판단하게 됩니다. (일반적으로 FAST-9, 연속적인 n=9n = 9개의 픽셀 조건이 가장 성능이 좋다고 알려져 있음)
이러한 방법은 점 pp가 코너로 분류되면, pp와 인접한 점들도 코너점으로 검출될 확률이 높습니다. 이를 방지하기 위해서 non-maximal suppression에 해당하는 후처리를 진행합니다. 인접한 점들이 검출될 경우 코너성이 가장 큰 점만 남기고 나머제를 제거하게 됩니다.
V=max⁡{∑x∈State ∣x−p∣−t,∑x∈Sderi ∣p−x∣−t}V=\max \left\{\sum_{x \in S_{\text {tate }}}|x-p|-t, \sum_{x \in S_{\text {deri }}}|p-x|-t\right\}
각 점들에 대해 VV값을 계산한 뒤, 자신보다 높은 VV값을 가지는 점이 있으면, 그 점을 제거합니다.

Reference

Made with