Linear Algebra
///
///
🥎

EPro-PnP 읽어보기

생성일
2022/06/29 10:41
태그
pose estimation
PnP

** Best Student Paper Award in CVPR 2022

EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimation

Pose Estimation이 뭔가요?

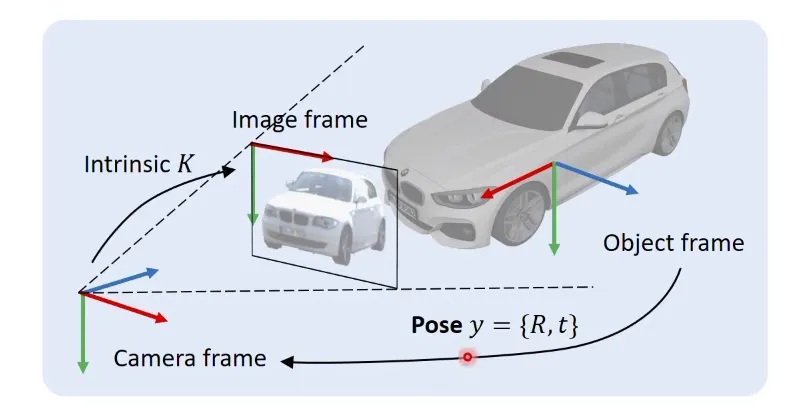
이 task의 목표는 Object Frame에서 Camera Frame으로의 Transformation을 구하는 것이다. 이 때, 구하고자 하는 Transformation을 나타낼 때, Object Pose y={R,t}y = \left\{ R,t\right\} 로 나타낸다. RR 은 Orientation을 나타내는 3×33 \times 3 Rotation Matrix 이고, tt 는 Position을 나타내는 3×13 \times 1 Translation Vector입니다.따라서 어떻게 하면 pose yy 를 정확하게 구할 수 있을지를 고민한다.

Pose Estimation을 푸는 방법에는 어떤게 있나요?

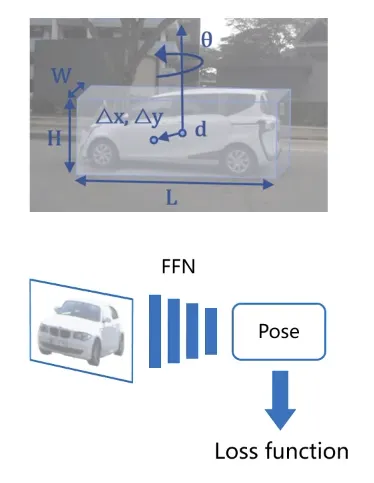
1. Direct Pose Prediction

3차원 Object Detection Task에서 자주 사용되는 방법!
2차원 이미지를 input으로 사용하고, 그에 해당하는 실제 사물의 pose를 training data로 주어서 단순한 End-to-End Network를 구성하여 Pose를 추정하는 방법이다.

단점은…?

하나의 네트워크만 달랑 만들어서 추정하기 때문에 블랙박스처럼 사용되어, 함수가 수행하는 기능을 구체적으로 명시하기가 어렵습니다. (Interpretability가 부족하다) 또한 Overfitting Issue에 취약한 단점을 지닙니다.
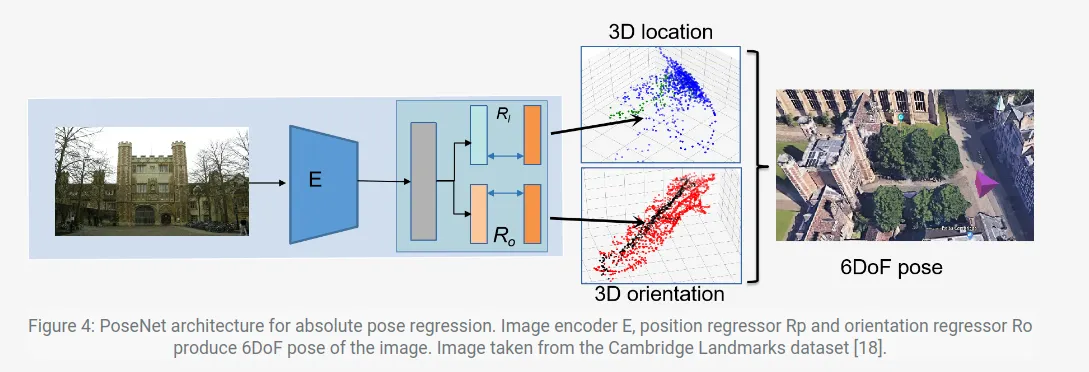
ex) PoseNet: A Convolutional Network for Real-Time 6-DOF Camera Relocalization
ICCV 2015 Open Access Repository
PoseNet: A Convolutional Network for Real-Time 6-DOF Camera Relocalization Alex Kendall, Matthew Grimes, Roberto Cipolla ; Proceedings of the IEEE International Conference on Computer Vision (ICCV), 2015, pp. 2938-2946 We present a robust and real-time monocular six degree of freedom relocalization system.
https://openaccess.thecvf.com/content_iccv_2015/html/Kendall_PoseNet_A_Convolutional_ICCV_2015_paper.html

2. Geometry-based Pose Estimation (Perspective-n-Point)

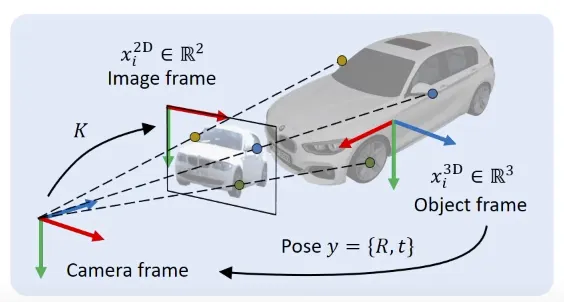
object의 shape을 알고 있는 가정에서 진행하는 6DoF pose estimation task에서 사용된다. 딥러닝 방식과는 달리 3D Geometry에서 각 요소들끼리의 관계를 이용해 풀어내는 방법이다.
아래와 같이 N개의 3d-2d 매칭쌍들을 찾은 뒤에 Object Pose yy 를 추정하는 방식이다!
xi3D∈R3,xi2D∈R2,wi2D∈R+2x_{i}^{3 \mathrm{D}} \in \mathbb{R}^{3}, \quad x_{i}^{2 \mathrm{D}} \in \mathbb{R}^{2}, \quad w_{i}^{2 D} \in \mathbb{R}_{+}^{2}
이러한 PnP 문제를 푸는 방법에는 DLT(Direct Linear Transform), P3P, EPnP, UPnP 등등이 존재!
Object Pose는 아래의 Optimization 문제를 해결함으로써 구할 수 있습니다.
Minimize cumulative squared weighted Reprojection Error
arg⁡min⁡y12∑iN∥fi(y)∥2fi(y)=wi2D∘(π(Rxi3D+t)−xi2D)\underset{y}{\arg \min } \frac{1}{2} \sum_{i}^{N}\left\|f_{i}(y)\right\|^{2}\\ f_{i}(y)=w_{i}^{2 \mathrm{D}} \circ\left(\pi\left(R x_{i}^{3 \mathrm{D}}+t\right)-x_{i}^{2 \mathrm{D}}\right)

3. PnP Combined with Deep Learning

최근에는 앞서 다룬 두 방법을 융합한 방법이 등장하고 있다. 앞단에서는 딥 네트워크를 사용하고, 뒷단에서는 PnP를 사용합니다. 이전 방법에서는 네트워크를 통해 pose를 바로 추정하려고 했던 반면, 여기서는 네트워크를 통해 2D-3D 매칭쌍을 찾습니다. 그 후, PnP solver에 넣어 정확한 pose를 추정합니다.
이런 방식으로 사용하면 더 안정적인 성능을 얻을 수 있습니다!! (End-to-End 보단..)
[X][X] 가 의미하는 것은 매칭쌍이고, [y][y] 가 의미하는 것은 pose입니다!! (잊지말자, 계속 나옴)

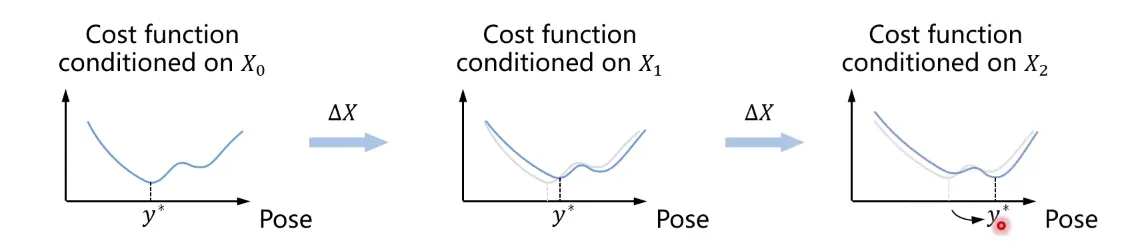
문제정의. 하지만, 딥 네트워크를 통해 얻은 2D-3D 매칭쌍 정보가 최적의 값이라고 보장할 수는 없습니다.

앞단에서 구한 2D-3D 매칭쌍이 정확하다고 말할 수 없기 때문에, 뒷단에서 PnP를 통해 얻는 Pose y∗y^* 역시 정확하지 않고 불안정한 값을 갖게 됩니다.
따라서, 위 Reprojection Error term을 최소로 하기 위해서는 argmin function을 미분하여 0이 되도록 만들어야 하는데, 앞단에서 안정적이지 않은 training 때문에, argmin function이 미분이 불가능해집니다.

Q. 왜 미분이 불안정한지 조금 더 설명해 주세요

Unstable backpropagation through “argmin” ← 이 논문이 나오게 되는 계기!
매칭쌍 XX 가 변하는 것에 맞춰 y∗y^* 또한 변하는데, 때때로 Global Optimum이 급격히 변하기 때문에 y∗y^* 의 변화가 discontinuous 한 경우가 생긴다. → 미분이 불가능해짐!

Proposed: End-to-End Probabilistic PnP

그래서 pose yy 를 안정적으로 추정하기 위해서, 다음과 같은 방법을 제시합니다.
pose를 고정적인 하나의 값으로 표현하지 않고, 확률 분포의 형태로 표현하는 것입니다.
pose를 확률 분포로 나타내게 되면, 기본적으로 연속적이기 때문에 미분이 가능해 집니다. 이를 이용해 일반적인 argmin function을 미분가능한 softargmin으로 대체합니다
먼저 likelihood function을 cumulative reprojection error를 기본으로 하여 만든다.
p(X∣y)=exp⁡−12∑iN∥fi(y)∥2 p(X \mid y)=\exp -\frac{1}{2} \sum_{i}^{N}\left\|f_{i}(y)\right\|^{2}
구하고자 하는 분포는 p(y∣X)p(y \mid X) 이므로, Bayes theorem을 이용하여 구한다. (+ uniformative prior)
아래 분포가 일반적인 softmax의 표현과 같기 때문에, softargmax라고 부르는 것 같다.
p(y∣X)=p(X∣y)∫p(X∣y)dy=exp⁡−12∑iN∥fi(y)∥2∫exp⁡−12∑iN∥fi(y)∥2 dyp(y \mid X)=\frac{p(X \mid y)}{\int p(X \mid y) \mathrm{d} y}=\frac{\exp -\frac{1}{2} \sum_{i}^{N}\left\|f_{i}(y)\right\|^{2}}{\int \exp -\frac{1}{2} \sum_{i}^{N}\left\|f_{i}(y)\right\|^{2} \mathrm{~d} y}
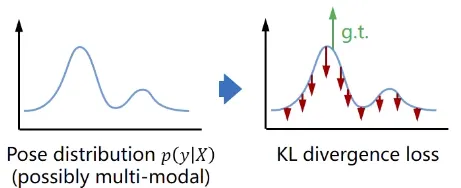
determinisitic pose yy 가 Probability Density p(y∣X)p(y \mid X) 로 대체 되었으므로, Loss function 또한 바뀌게 됩니다. 이 때, 두 확률분포의 차이를 계산하는데 사용하는 KL-Divergence를 사용하여 loss를 구합니다. loss를 구하기 위해 필요한 정답의 분포는 주어지는 Ground-Truth Pose를 이용하여 target pose distribution을 정의할 수 있으며 이를 t(y)t(y) 로 정합니다.
L=DKL(t(y)∣p(y∣X))=−∫t(y)log⁡p(X∣y)dy+log⁡∫p(X∣y)dy\begin{aligned}L &=D_{K L}(t(y) \mid p(y \mid X)) \\&=-\int t(y) \log p(X \mid y) \mathrm{d} y+\log \int p(X \mid y) \mathrm{d} y\end{aligned}
target과 prediction의 KL divergence의 값을 minimize함으로써 Global Convergence를 만족합니다.
그림으로 살펴보면, p(y∣X)p(y \mid X) 의 여러 개의 modal이 존재할 수 있으며, 이런 modal을 위에서 본 loss function을 이용해 억제하여 정확한 pose의 분포를 띄도록 만듭니다.
(Cross Entropy의 Continuous Version)

Q. 그렇다면 target 과 prediction Loss 의 분포를 어떻게 표현하죠?

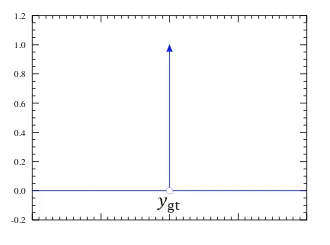
target loss는 쉽습니다! dirac delta function 같은 분포를 띈다고 가정합니다. 그래프로 표현하면 아래와 같고, ygty_{gt} 의 값만 1로 나타나고, 나머지 부분은 0이 됩니다.
이를 통해 아래와 같은 단순화된 Loss Function을 작성할 수 있습니다.
L=12∑iN∥fi(ygt)∥2⏟Ltgt+log⁡∫exp⁡−12∑i=1N∥fi(y)∥2 dy⏟LpredL=\underbrace{\frac{1}{2} \sum_{i}^{N}\left\|f_{i}\left(y_{\mathrm{gt}}\right)\right\|^{2}}_{L_{\mathrm{tgt}}}+\underbrace{\log \int \exp -\frac{1}{2} \sum_{i=1}^{N}\left\|f_{i}(y)\right\|^{2} \mathrm{~d} y}_{L_{\mathrm{pred}}}
predicted loss의 경우 Adaptive Multiple Importance Sampling (AMIS) 알고리즘을 이용해 Monte Carlo Pose Loss로 치환합니다.
Lpred ≈log⁡1K∑j=1Kexp⁡−12∑i=1N∥fi(yj)∥2q(yj)⏟vj (importance weight) ,L_{\text {pred }} \approx \log \frac{1}{K} \sum_{j=1}^{K} \underbrace{\frac{\exp -\frac{1}{2} \sum_{i=1}^{N}\left\|f_{i}\left(y_{j}\right)\right\|^{2}}{q\left(y_{j}\right)}}_{v_{j} \text { (importance weight) }},
두 분포를 실질적으로 표현하였으니, 이제 Backpropagation을 진행해 보자,
이에 대한 Loss Function의 Gradient를 구하면, 왼쪽 항에서는 target pose의 reprojection error의 gradient이고, 오른쪽 항에서는 predicted pose의 reprojection error의 기댓값으로 나타납니다.
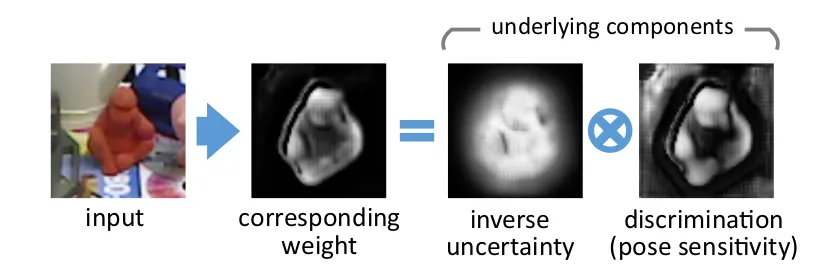
∂L∂(⋅)=∂∂(⋅)12∑iN∥fi(ygt)∥2−Ey∼p(y∣X)∂∂(⋅)12∑i=1N∥fi(y)∥2\frac{\partial L}{\partial(\cdot)}=\frac{\partial}{\partial(\cdot)} \frac{1}{2} \sum_{i}^{N}\left\|f_{i}\left(y_{\mathrm{gt}}\right)\right\|^{2}-\underset{y \sim p(y \mid X)}{\mathbb{E}} \frac{\partial}{\partial(\cdot)} \frac{1}{2} \sum_{i=1}^{N}\left\|f_{i}(y)\right\|^{2}
앞서 reprojection 과정에서 weighted correspondence를 사용하였는데, 최적의 pose를 얻기 위해 이 weight wi2D{ w_{i}^{2 \mathrm{D}}} 에 대해 미분을 진행해보자.
−∂LKL∂wi2D=wi2D∘(−ri∘2(ygt)+Ey∼p(y∣X)ri∘2(y))-\frac{\partial L_{\mathrm{KL}}}{\partial w_{i}^{2 \mathrm{D}}}=w_{i}^{2 \mathrm{D}} \circ\left(-r_{i}^{\circ 2}\left(y_{\mathrm{gt}}\right)+\underset{y \sim p(y \mid X)}{\mathbb{E}} r_{i}^{\circ 2}(y)\right)
ri(y)=π(Rxi3D+t)−xi2D r_{i}(y)=\pi\left(R x_{i}^{3 \mathrm{D}}+t\right)-x_{i}^{2 \mathrm{D}}
−ri∘2(ygt) -r_{i}^{\circ 2}\left(y_{\mathrm{gt}}\right)\ 항이 의미하는 것은 큰 reprojection error를 가지는 weight는 값을 줄여야 합니다. → Correspondences with large reprojection error should be weighted less → Correspondences with small reprojection error should be weighted more (Uncertainty)
Ey∼p(y∣X)ri∘2(y)\underset{y \sim p(y \mid X)}{\mathbb{E}} r_{i}^{\circ 2}(y) 항이 의미하는 것은 predicted pose의 reprojection error의 분산과 관계된 요소입니다. → sensitive correspondences should be weighted more (Discrimination)

따라서 Uncertainty 와 Discrimination의 균형을 잡는것이 중요합니다!

LtgtL_{tgt} : Minimize the reprojection error at the true pose, making the weighted point aware of reprojection Uncertainty
→ 높은 confidence를 가지는 안쪽 지역 point에 더 많은 weight를 준다!
LpredL_{pred} : Maximize the reprojection error over the predicted pose, s.t. the weighted points are discrimnative to wrong pose
→ pose 변화에 민감한 가장자리 쪽 지역 point에 더 많은 weight를 준다!

이러한 두 가지 요소를 결합하여 이미지에서 중요한 지역에 더 집중할수 있도록 만들어 준다!

Experimental Result

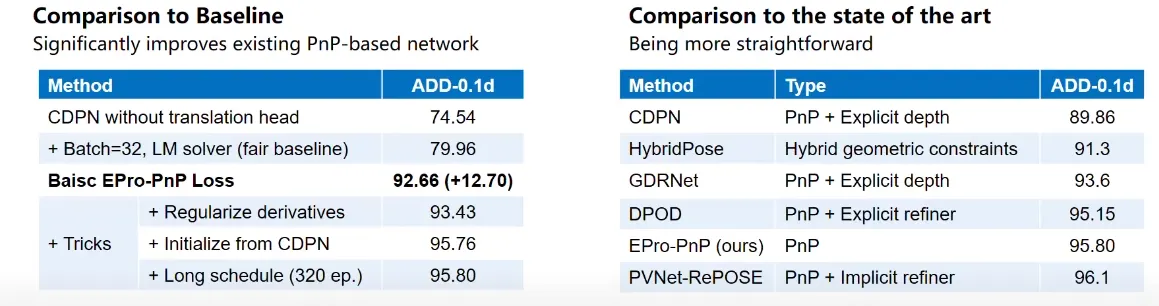
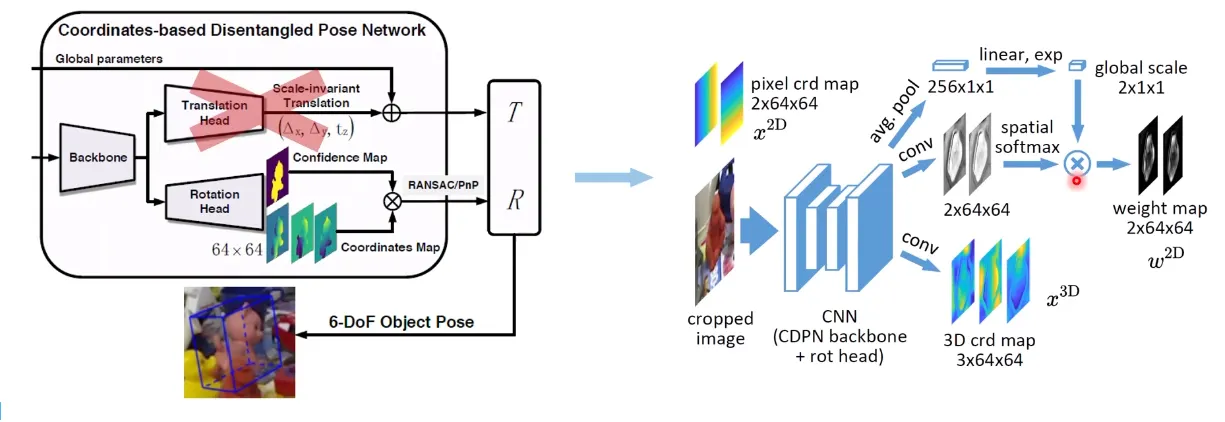
위에서 제시한 EPro-PnP layer가 실제로 성능을 향상 시키는지 확인하기 위해 기존에 존재했던 PnP-based Network에 넣어 확인합니다. 여기서 사용한 네트워크는 CDPN이라는 네트워크입니다.
CDPN: Coordinates-Based Disentangled Pose Network for Real-Time RGB-Based 6-DoF Object Pose Estimation
6-DoF object pose estimation from a single RGB image is a fundamental and long-standing problem in computer vision. Current leading approaches solve it by training deep networks to either regress both rotation and translation from image directly or to construct 2D-3D correspondences and further solve them via PnP indirectly.
https://ieeexplore.ieee.org/document/9009519
pose accuracy를 향상 시켰다.

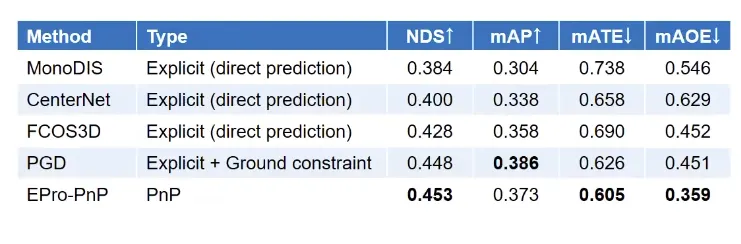
추가로….

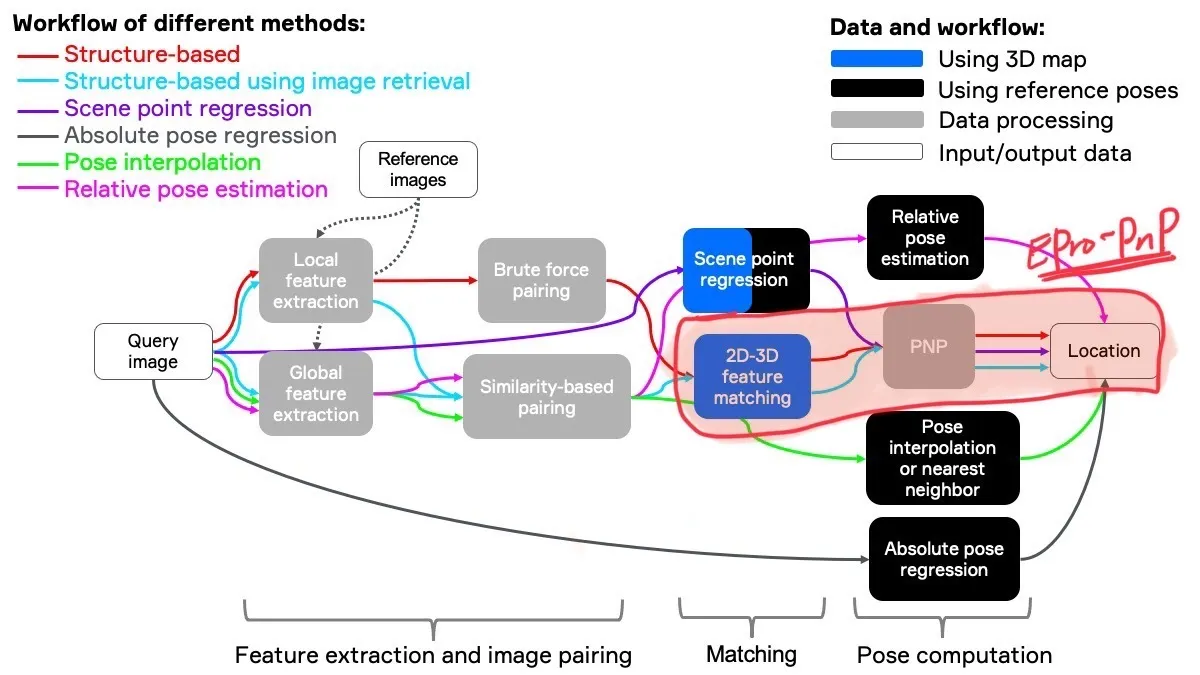
이 논문이 사용될 수 있는 분야는 Visual Localization 라는 분야인데,
Visual localization, a way to determine location from images, is a method used by robots and self-driving cars to estimate their position.
이 논문이 효력을 발휘할 수 있는 파이프라인은 아래와 같다!

Reference

CVPR 2022 Best Student Paper - EPro-PnP: End-to-End Probabilistic Perspective-n-Point
EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose EstimationI'm thrilled that our paper has been awarded the Best...
https://www.youtube.com/watch?v=TonBodQ6EUU
EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimation
Locating 3D objects from a single RGB image via Perspective-n-Points (PnP) is a long-standing problem in computer vision. Driven by end-to-end deep learning, recent studies suggest interpreting PnP as a differentiable layer, so that 2D-3D point correspondences can be partly learned by backpropagating the gradient w.r.t. object pose.
https://arxiv.org/abs/2203.13254
Methods for visual localization
Blog post. By dissecting the matching process of the recent ColBERT model, we make a step towards unveiling the ranking properties of BERT-based ranking models.
https://europe.naverlabs.com/blog/methods-for-visual-localization/
Made with