Linear Algebra
///
///
⛄

4. Preliminaries for SVD

태그
SVD
Multiplicity
Spectral Theorem
Quadratic Form

EVD와 SVD의 차이

Eigenvalue Decomposition의 경우 n×nn \times n square matrix를 대상으로 하는 반면에, Singular Value Decomposition은 m×nm \times n 크기의 rectangular matrix를 대상으로 한다. 일반적으로 SVD의 경우 m×nm \times n 크기의 행렬 AA를 AA⊤,A⊤AAA^{\top}, A^{\top}A 하여 square matrix 형태로 만든후 EVD를 실행하는 것이다.

Algebraic/Geometric Multiplicity

앞선 포스트를 통해 n개의 linearly independent한 eigenvector가 존재한다면 Diagonalizable하다는 것을 배웠다. 그렇다면 어떤 상황에서 n개의 linearly independent한 eigenvector를 뽑을 수 있을까?
일반적으로 det⁡(A−λI)=0\operatorname{det}(A-\lambda I)=0 를 진행하여 나올수 있는 근의 전체 개수는 행렬 A의 column 개수 n개이다. 하지만 (1) n개중 에서 허근이 있다면? n개의 linearly independent한 eigenvector를 뽑을 수 없게 된다. 또한 중근이 존재한다면 그 eigenvalue에 해당하는 eigenvector가 2개 나올 수 있으며, 만약 (2) 이 두 개가 Linearly dependent한 경우에도 n개의 linearly independent한 eigenvector를 뽑을 수 없다.
Algebraic Multiplicity는 특성방정식으로 표현할 때 나오는 중근의 개수를 말하고, Geometric Multiplicity는 동일한 λ\lambda에 대하여 linearly independent한 eigenvector의 개수를 말한다.
예를 들어, (λ−1)2(λ+5)=0(\lambda-1)^{2}(\lambda+5)=0 라는 특성 방정식이 주어졌을 때 각 eigenvalue에 대한 multiplicity를 표로 정리하면 아래와 같다.
비교
lambda = 0
lambda = -5
A.M
2
1
G.M
2여야 함!
1
이 때, A.M > G.M 인 경우, 전체 가질 수 있는 eigenvector의 개수를 충족하지 못하므로, eigendecomposition이 불가능 해진다.

The Spectral Theorem

n×nn \times n symmetric matrix인 행렬 AA가 주어졌을 때, 아래 성질을 가집니다!
•
행렬 AA는 nn개의 실수 eigenvalue를 가집니다.(multiplicity 고려해서)
•
각 eigenvalue λ\lambda에 대한 eigenspace의 dimension은 특성 방정식에서의 근 λ\lambda의 multiplicity와 같습니다. (Geometric Multiplicity == Algebraic Multiplicity)
•
각 λ\lambda에 해당하는 eigenspace는 서로 orthogonal합니다. 즉, eigenvalue가 다른 eigenvector들은 서로 orthogonal 합니다.
•
위의 성질을 만족하는 행렬 AA는 orthogonally diagonalizable 합니다.

Orthogonal Matrix란?

아래 두 조건을 만족하는 행렬을 말한다.
•
행렬을 구성하는 row vector 혹은 column vector의 길이가 1이다.
•
각 row vector 또는 column vector들이 서로 수직이다.
위 조건을 통해 아래 수식을 만족하게 되고, 이를 통해 쉽게 역행렬을 구할 수 있습니다.
AA⊤=A⊤A=IAA^{\top} = A^{\top}A = I
이러한 Orthogonal matrix의 성질에는 크게 4가지가 존재합니다.
•
Orthogonal Matrix를 Transpose 해도 Orthogonal Matrix 입니다.
•
Orthogonal Matrix의 역행렬 또한 Orthogonal Matrix 입니다.
•
Orthogonal Matrix 끼리의 곱의 결과도 Orthogonal Matrix입니다.
•
Orthogonal Matrix의 Determinent는 1 또는 -1입니다.

Orthogonally Diagonalizable하다는 것의 의미?

말 그대로 orthogonal한 성질을 가지면서 diagonalize를 할 수 있다는 것이다.
•
diagonalizable ⇒ eigen decomposition이 가능하다.
•
orthogonal ⇒ distinct한 eigenvalue에 대해서는 eigenvector가 orthogonal합니다. 그러나 같은 eigenvalue에 해당하는 eigenvector끼리는 orthogonal하지 않을 수 있는데, 이를 위해 QR-decomposition을 활용해 서로 orthogonal하게 만든다.

Quadratic Form의 변수 변경하기

Quadratic form은 Rn\mathbb{R}^{n} 공간상의 함수 QQ를 말하며, 아래의 식으로 표현될 때 정의할 수 있다. 이 때 행렬 AA는 n×nn \times n symmetric matrix이다.
Q(x)=xTAxQ(\mathbf{x})=\mathbf{x}^{T} A \mathbf{x}
이러한 Quadratic form을 이용해서 임의의 식으로 주어졌을 때, 행렬의 곱의 형태로 표현 가능하다.
Q(x)=6x12+4x22+8x32−x1x2+8x2x3Q(\mathbf{x})=6 x_{1}^{2}+4 x_{2}^{2}+8 x_{3}^{2}-x_{1} x_{2}+8 x_{2} x_{3}
Q(x)=xTAx=[x1x2x3][6−1/20−1/244048][x1x2x3]Q(\mathbf{x})=\mathbf{x}^{T} A \mathbf{x}=\left[\begin{array}{lll}x_{1} & x_{2} & x_{3}\end{array}\right]\left[\begin{array}{ccc}6 & -1 / 2 & 0 \\-1 / 2 & 4 & 4 \\0 & 4 & 8\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2} \\x_{3}\end{array}\right]
이러한 Quadratic form에는 중요한 성질이 있는데, 아래와 같다.
행렬 AA가 n×nn \times n symmetric matrix라고 가정하였을 때, 변수 x=Py\mathbf{x}=P \mathbf{y}를 orthogonal changing 한다. 이러한 변환은 quadratic form Q(x)=xTAxQ(\mathbf{x})=\mathbf{x}^{T} A \mathbf{x}로 하여금 yTDy\mathbf{y}^{T} D \mathbf{y}의 형태로 바뀌게 하며, 행렬 DD는 cross-product term이 없고 행렬 AA의 eigenvalue로만 이루어진 diagonal matrix이다.
이 때, 행렬 PP의 column들은 Q(x)=xTAxQ(\mathbf{x})=\mathbf{x}^{T} A \mathbf{x}의 quadratic form의 principal axes라고 불리운다. 식으로 유도한다면, xTAx=(Py)TA(Py)=yTPTAPy=yT(PTAP)y\mathbf{x}^{T} A \mathbf{x}=(P \mathbf{y})^{T} A(P \mathbf{y})=\mathbf{y}^{T} P^{T} A P \mathbf{y}=\mathbf{y}^{T}\left(P^{T} A P\right) \mathbf{y}와 같이 표현되며, 행렬 AA가 symmetric 하기 때문에, PTAP=DP^{T} A P = D를 만족시키는 eigenvalue로 이루어진 행렬 DD가 반드시 존재한다.
이런 변환을 함으로써 어떠한 quadratic form으로 주어져도 cross-product이 없는 형태의 quadratic form으로 바꿀 수 있다. (변환의 가장 큰 이유!!!)
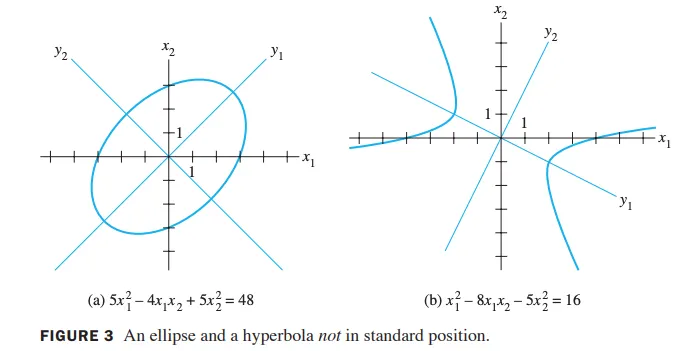
이러한 변환을 기하학점 관점에서 살펴보면 다음과 같다.
3-(a)의 경우를 보면 Q(x)=5x12−4x1x2+5x22=48Q(\mathbf{x})=5 x_{1}^{2}-4 x_{1} x_{2}+5 x_{2}^{2}=48 의 식을 변환을 하게 되면, yTDy=3y12+7y22\mathbf{y}^{T} D \mathbf{y}=3 y_{1}^{2}+7 y_{2}^{2}의 꼴로 바뀌며, 바꾸는데 사용한 행렬 P=[u1u2]=[1/2−1/21/21/2]P=\left[\begin{array}{ll} \mathbf{u}_{1} & \mathbf{u}_{2} \end{array}\right]=\left[\begin{array}{rr} 1 / \sqrt{2} & -1 / \sqrt{2} \\ 1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right]의 column들이 새로운 좌표계의 basis vector가 됨을 알 수 있다!

Quadratic Form 분류하기

Quadratic form QQ는 아래 3가지로 분류한다.
•
positive definite  if Q(x)>0 for all x≠0\text { if } Q(\mathbf{x})>0 \text { for all } \mathbf{x} \neq \mathbf{0}
•
negative definite  if Q(x)<0 for all x≠0\text { if } Q(\mathbf{x})<0 \text { for all } \mathbf{x} \neq \mathbf{0}
•
indefinite  if Q(x) assumes both positive and negative values. \text { if } Q(\mathbf{x}) \text { assumes both positive and negative values. }
0을 포함하는 경우, positive semi-definite if Q(x)≥0 for all x\text { if } Q(\mathbf{x}) \geq 0 \text { for all } \mathbf{x}, negative semi-definite  if Q(x)≤0 for all x\text { if } Q(\mathbf{x}) \leq 0 \text { for all } \mathbf{x} 라고 정의한다.
위와 같은 분류를 eigenvalue와의 연관성을 고려한다면 아래와 같이 서술 할 수 있다!
행렬 AA가 n×nn \times n symmetric matrix라고 가정하였을 때, quadratic form xTAx\mathbf{x}^{T} A \mathbf{x}는
•
positive definite하다는 것은 행렬 AA의 eigenvalue들이 모두 양수이다는 것과 동치이다.
•
negative definite하다는 것은 행렬 AA의 eigenvalue들이 모두 음수이다는 것과 동치이다.
•
indefinite하다는 것은 행렬 AA의 eigenvalue들이 양수 또는 음수로 이루어져있다는 것과 동치이다.

Constrained Optimization

행렬 AA가 symmetric matrix라고 가정하고, 값 m,nm,n을 아래와 같이 정의할 때
m=min⁡{xTAx:∥x∥=1},M=max⁡{xTAx:∥x∥=1}m=\min \left\{\mathbf{x}^{T} A \mathbf{x}:\|\mathbf{x}\|=1\right\}, \quad M=\max \left\{\mathbf{x}^{T} A \mathbf{x}:\|\mathbf{x}\|=1\right\}
mm은 행렬 AA의 가장 작은 eigenvalue와 같고, 이 때의 x\mathbf{x}는 그에 해당하는 eigenvector일 때이다. 반대로, MM은 행렬 AA의 가장 큰 eigenvalue와 같고, 이 때의 x\mathbf{x}는 그에 해당하는 eigenvector일 때이다.
→ svd로 해를 구할 때 사용 (Ax=0Ax = \mathbf{0}를 풀 때 사용)

Reference

Linear Algebra and Its Applications
Buy Linear Algebra and Its Applications on Amazon.com ✓ FREE SHIPPING on qualified orders
https://www.amazon.com/Linear-Algebra-Its-Applications-5th/dp/032198238X
Made with