Linear Algebra
//
//
🏉

An introduction to inertial navigation

www.cl.cam.ac.uk
https://www.cl.cam.ac.uk/techreports/UCAM-CL-TR-696.pdf

Inertial Navigation의 기본적인 내용과, Error Characteristic을 간단히 정리한다.

위 자료를 참고하여 제작하였다. 더 자세히 살펴보고 싶은 분들은 직접 읽어보기를 권장한다.

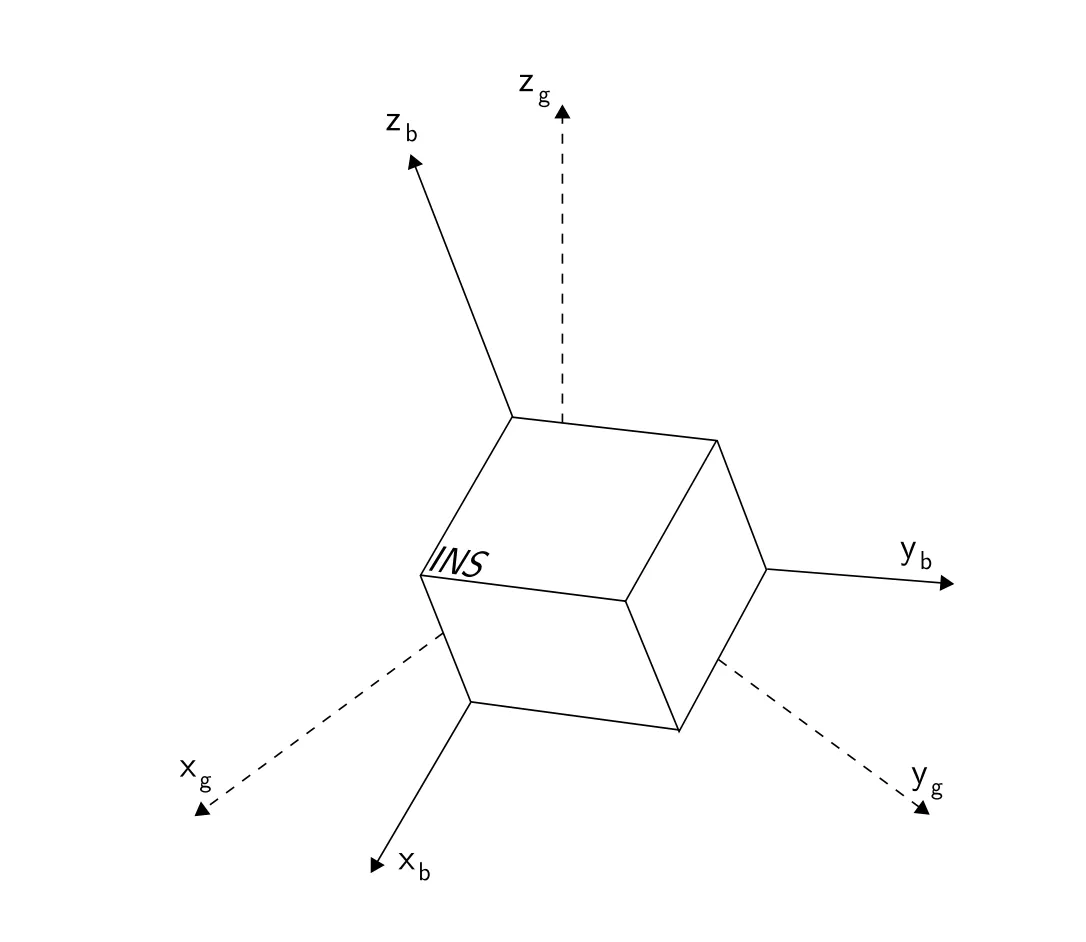
IMU sensor의 reference frame

body frame과 global frame 2가지로 구분하여 다룬다.

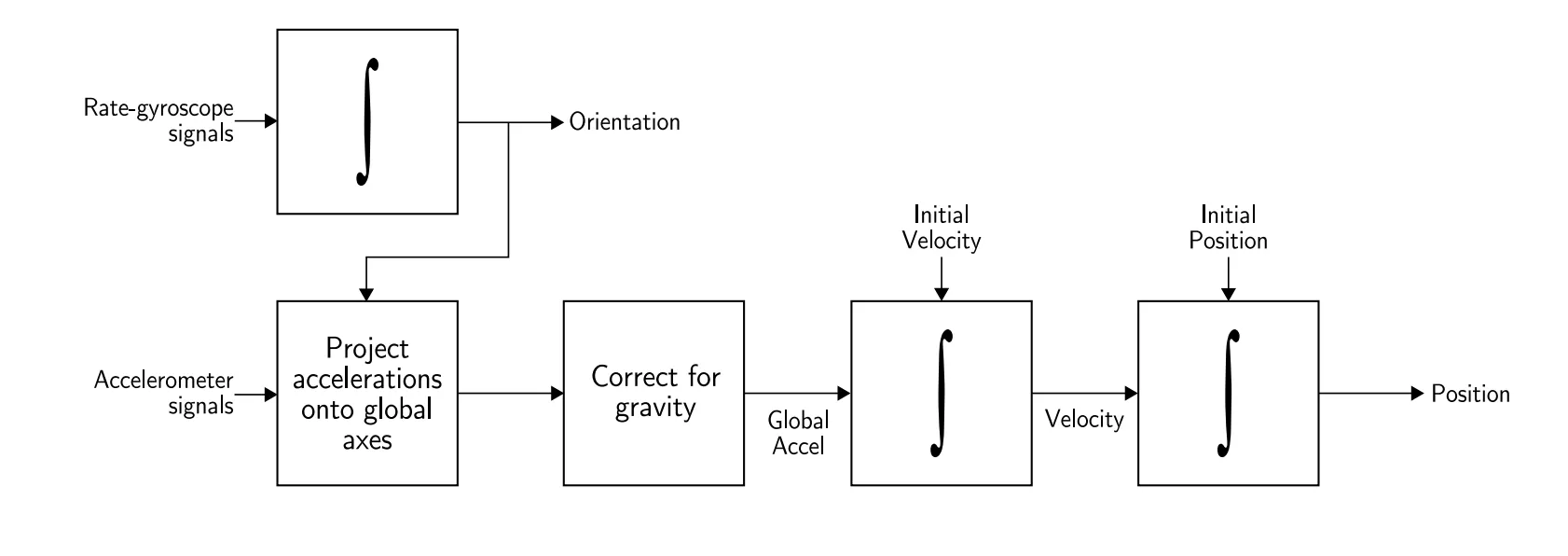
Strap-down Systems

이 시스템 상에서, inertial sensor들은 디바이스에 rigidly하게 연결되어 있기 때문에, Output quantities는 주로 body frame에서 측정된 값이 나타난다.
•
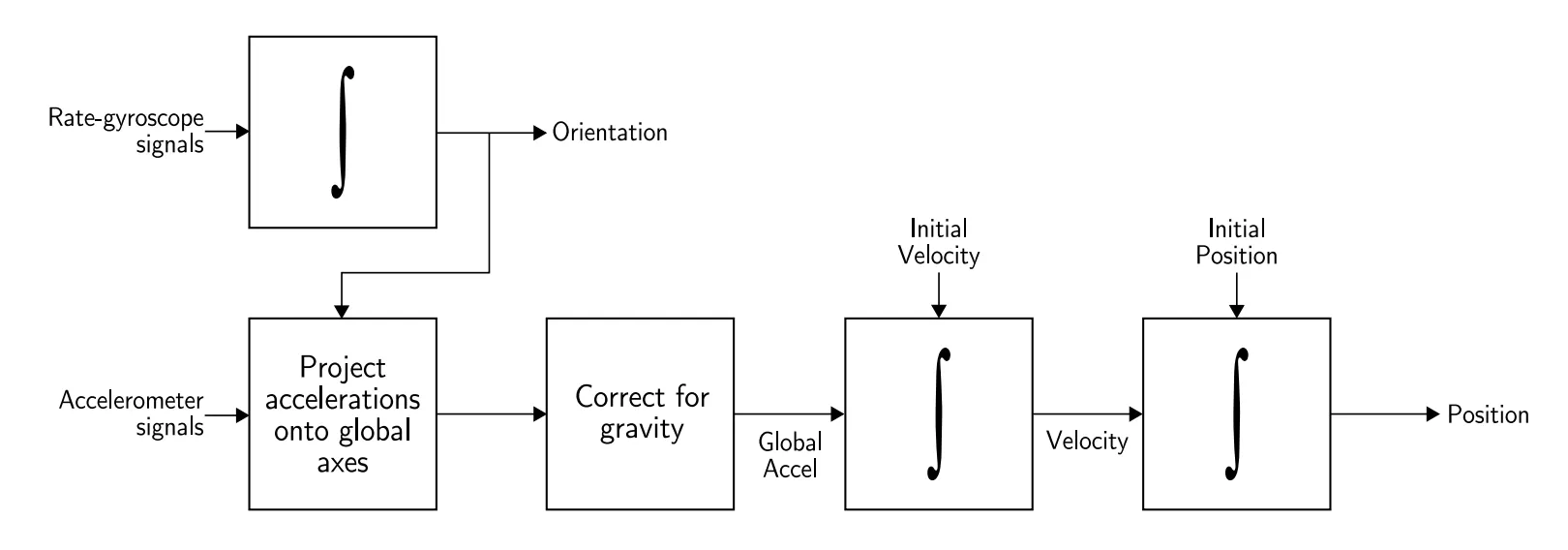
Orientation : rate-gyroscope에서 얻은 신호를 Integration 한다.
•
Position : 앞에서 구한 Orientation 정보를 이용하여 accelerometer에서 얻은 신호를 global coordinates로 변환하고 그것을 Double-Integration 한다.

Gyroscopes

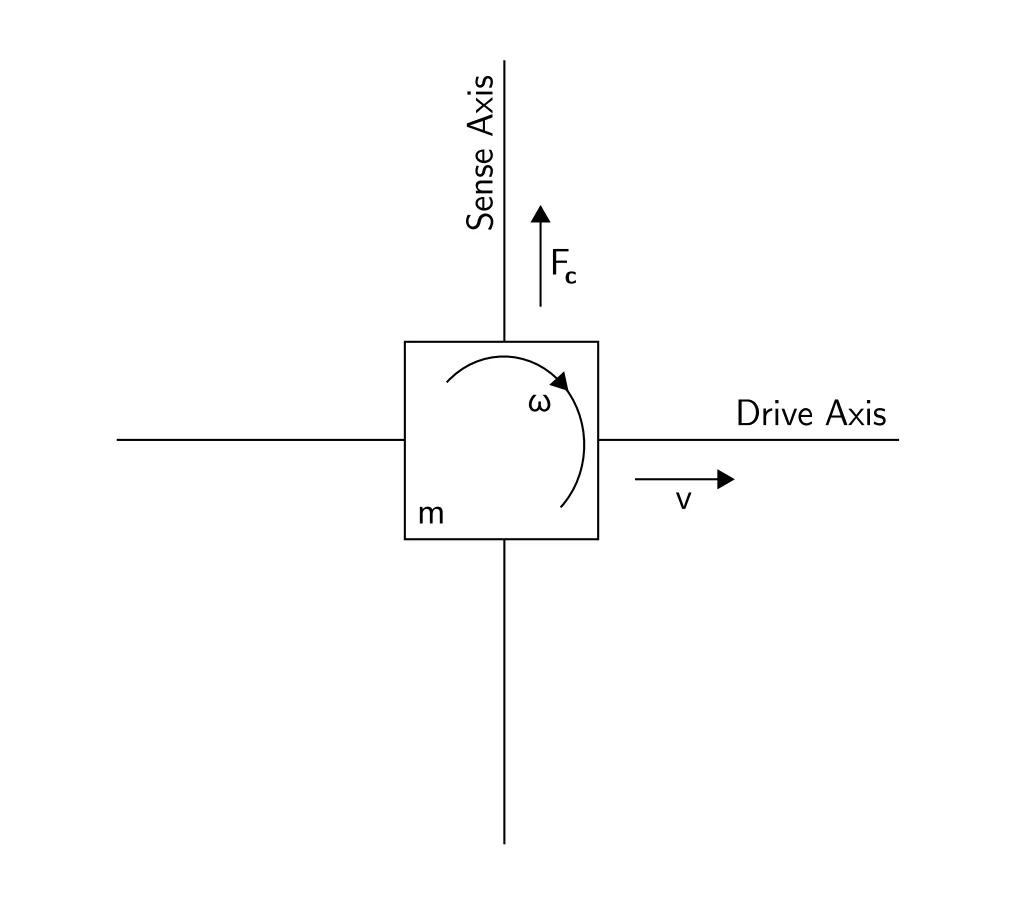
MEMS Gyroscopes의 경우, Coriolis effect 를 이용하여 angular-velocity를 구한다.
이 효과는 회전체의 표면 위에서 운동하는 물체에 대하여 운동 속도 방향에 수직으로 작용하는 가상의 힘이 생김을 나타내는데, 식으로 표현하면 아래와 같다.
Fc=−2m(ω×v)\boldsymbol{F}_c=-2 m(\boldsymbol{\omega} \times \boldsymbol{v})
MEMS Gyroscopes는 이러한 Coriolis effect 를 측정하기 위해 진동소자를 포함하고 있다. drive axis를 따라 단일 물체가 진동하도록 되어있다. Gyroscope가 회전할 때 Coriolis effect 에 의해 수직방향의 sense axis를 따라 2차 진동이 유도된다. angular velocity ω\boldsymbol{\omega} 는 이 2차 진동을 이용해 측정할 수 있다.

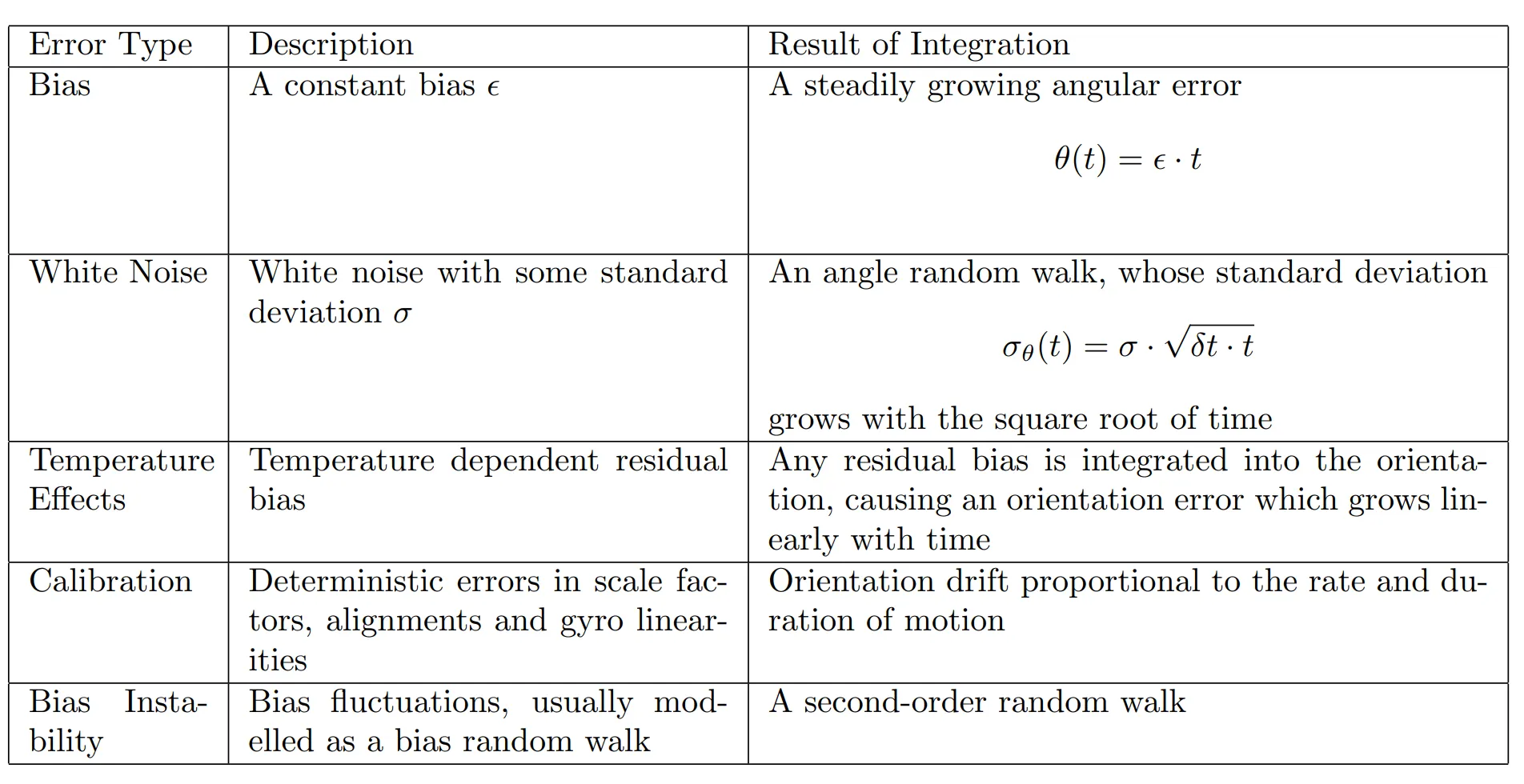
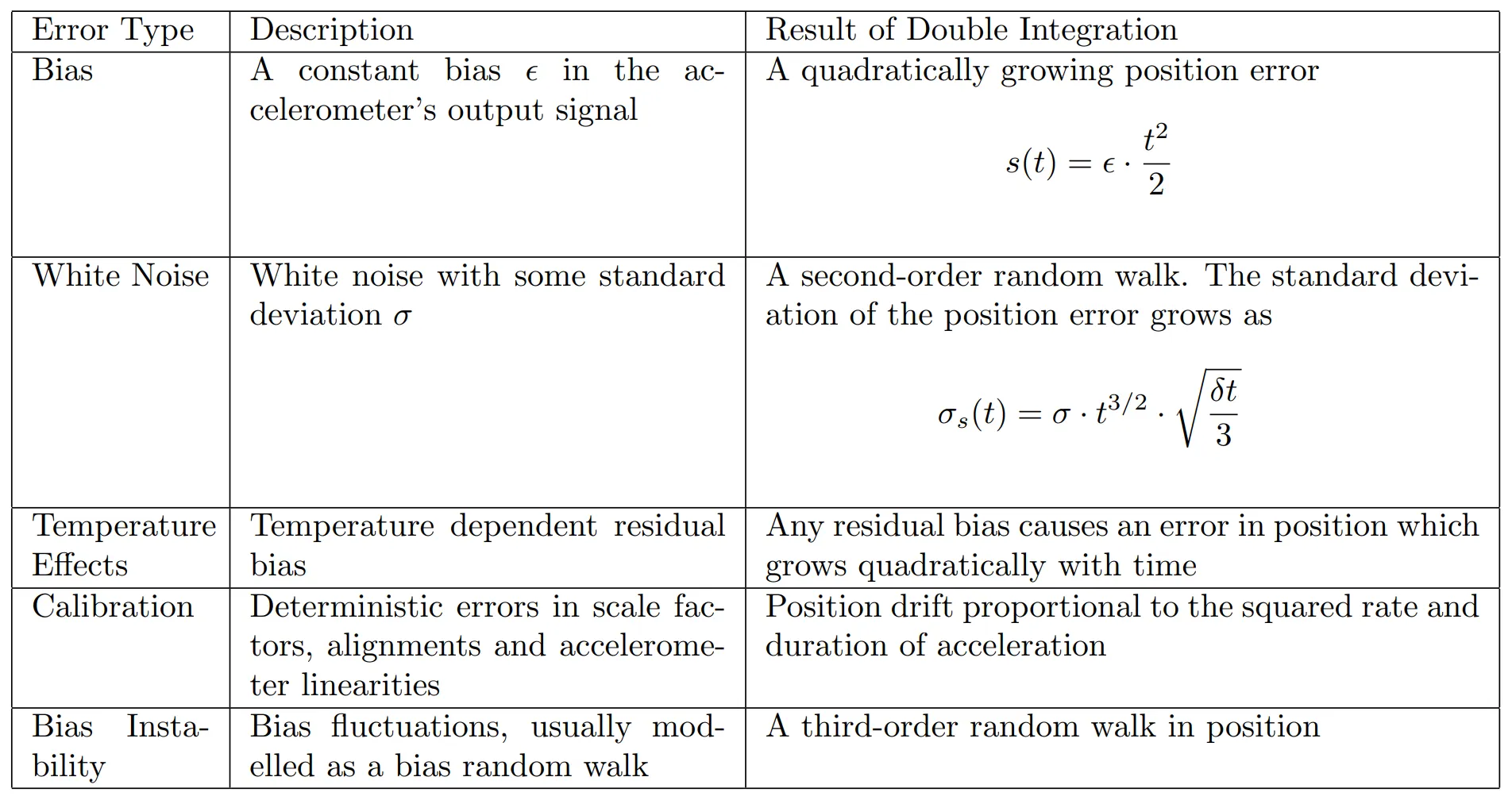
MEMS Gyro Error Characteristics

Accelerometers

2가지 방법으로 MEMS accelerometers를 다룬다
•
mechanical : 스프링과 연결된 mass를 이용하여 displacement를 측정한다.
•
Solid state : 입력 축을 따라 가속도가 가해지면 빔이 휘어집니다. 변형률에 비례하여 표면 음파의 주파수를 변화시키게 된다. 이러한 주파수 변화를 측정하여 가속도를 측정한다.

MEMS Accelerometers Error Characteristics

Strapdown Inertial Navigation

Tracking Orientation

C\boldsymbol{C} : global frame 과 body frame 간의 변환을 나타내는 회전 행렬
δtδt : 연속적인 samples 사이 시간 간격
σ=∣ωbδt∣\sigma=\left|\omega_b \delta t\right| , ωb=(ωbx,ωby,ωbz)T\boldsymbol{\omega}_b=\left(\omega_{b x}, \omega_{b y}, \omega_{b z}\right)^T
B=(0−ωbzδtωbyδtωbzδt0−ωbxδt−ωbyδtωbxδt0)\boldsymbol{B}=\left(\begin{array}{ccc}0 & -\omega_{b z} \delta t & \omega_{b y} \delta t \\\omega_{b z} \delta t & 0 & -\omega_{b x} \delta t \\-\omega_{b y} \delta t & \omega_{b x} \delta t & 0\end{array}\right)
C(t+δt)=C(t)(I+sin⁡σσB+1−cos⁡σσ2B2)\boldsymbol{C}(t+\delta t) =\boldsymbol{C}(t)\left(\boldsymbol{I}+\frac{\sin \sigma}{\sigma} \boldsymbol{B}+\frac{1-\cos \sigma}{\sigma^2} \boldsymbol{B}^2\right)

Tracking Position

vg\boldsymbol{v}_g : velocity
sg\boldsymbol{s}_g : displacement
vg(t+δt)=vg(t)+δt⋅(ag(t+δt)−gg)sg(t+δt)=sg(t)+δt⋅vg(t+δt)\begin{aligned}\boldsymbol{v}_g(t+\delta t) &=\boldsymbol{v}_g(t)+\delta t \cdot\left(\boldsymbol{a}_g(t+\delta t)-\boldsymbol{g}_g\right) \\\boldsymbol{s}_g(t+\delta t) &=\boldsymbol{s}_g(t)+\delta t \cdot \boldsymbol{v}_g(t+\delta t)\end{aligned}

Reducing drift in INS

1.
Sensor fusion → GPS, Magnetometers
2.
Domain Specific Assumptions
a.
IMU가 부착된 body의 움직임에 대해 가정하여 사용 NavShoe → 신발에 IMU를 부착하고, 발이 땅에 닿을 때에는 velocity를 0으로 가정 velocity drift가 주기적으로 교정된다.
b.
한정적인 환경에서만 알고리즘이 동작한다. 조금이라도 상황이 바뀌면 잘 작동하지 않는다.
Made with